Question

【题目】如图，在菱形ABCD中，AB=10，AC=16，点M是对角线AC上的一个动点，过点M作PQ⊥AC交AB于点P，交AD于点Q，将△APQ沿PQ折叠，点A落在点E处，当△BCE是等腰三角形时，AP的长为_____．

Answer 1

【答案】或．

【解析】连接BD交AC于O，由四边形ABCD是菱形，得到AC⊥BD，推出△AMP∽△AOB，①当CE=CB时，如图1，则CE=10，AE=6，AM=3，根据相似三角形的性质得到，可求得AP=；

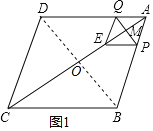
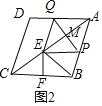
②当BE=EC时，如图2，点E是BC的垂直平分线与AC的交点，则CF=5，根据相似三角形的性质得到CE=，继而得出AE=16-=，然后可求出AM=，根据对应边的比求出AP=；

③当BC=BE时，E与A重合；
综上所述：当△BCE是等腰三角形时，AP的长为或．
故答案为：或．