题目内容
【题目】一只小虫子落在数轴上的某点
，第一次从
向左跳一个单位到
，第二次从向右跳
个单位到
，第三次从向左跳
个单位到
，第四次从向右跳
个单位到
，按以上规律跳了
次时，它落在数轴上的点
所表示的数恰好是2019，则这只小虫的初始位置所在的数是_____．
【答案】1969
【解析】
根据数轴上的点的移动规律：“左减右加”可分别用P0表示出P1、P2、P3，……，根据规律可表示出P100，由点
所表示的数恰好是2019即可求出P0表示的数，可得答案．
P1=P0-1，
P2=P1+2=P0-1+2，
P3=P2-3=P0-1+2-3，
……
P100=P0-1+2-3+4-……-99+100=P0+50，
∵点所表示的数恰好是2019，
∴P0=2019-50=1969，
∴这只小虫的初始位置
所在的数是1969，
故答案为：1969
【题目】（本小题满分10分）
问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成
种不同的等腰三角形，为探究
之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当
时，
用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当
时，
用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当
时，
用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当
时，
综上所述，可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二：
用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（只需把结果填在表②中）
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用
根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
（设分别等于
、
、
、
，其中
是整数，把结果填在表③中）
|
|
|
|
|
|
问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）
其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）
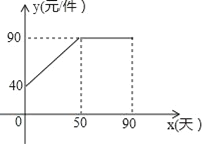
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
