��Ŀ����
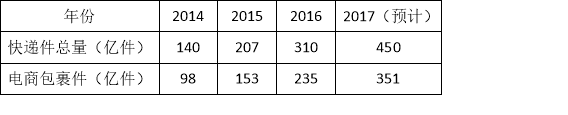
����Ŀ��Ϊ��ף���70���껪�������ⳬ�����ۼס���������ף��Ʒ���ó�����ͬʱ�����ס���������Ʒ��10��������400Ԫ;������������Ʒ30��������������Ʒ15��������ȥ750Ԫ��
��1����ס���������Ʒÿ���Ľ��ۣ�
��2�����ڼס���������Ʒ�ܵ�����ӭ��ʮһ�·ݳ��о��������ס���������Ʒ��80�����ұ��֣�1���Ľ��۲��䣬��֪������Ʒÿ�����ۼ�Ϊ15Ԫ��������Ʒÿ�����ۼ�40Ԫ��Ҫʹʮһ�·ݹ����ļס���������Ʒ��80��ȫ�������������������600Ԫ����ô�ó�������������Ʒ���ټ���
���𰸡���1��������Ʒÿ���Ľ���Ϊ10Ԫ��������Ʒÿ���Ľ���Ϊ30Ԫ����2���ó�������������Ʒ40��
��������
��1���������Ʒÿ���Ľ���ΪxԪ��������Ʒÿ���Ľ���ΪyԪ�����ݡ��ס���������Ʒ��10��������400Ԫ��������������Ʒ30��������������Ʒ15��������ȥ750Ԫ���ж�Ԫһ�η��������ɵã�
��2���蹺��������Ʒm������������Ʒ������80-m���������ݡ�80��ȫ�������������������600Ԫ���в���ʽ���ɵã�
�⣺��1���������Ʒÿ���Ľ���ΪxԪ��������Ʒÿ���Ľ���ΪyԪ��
�������⣬�ã�![]()
��ã�![]()
�𣺼�����Ʒÿ���Ľ���Ϊ10Ԫ��������Ʒÿ���Ľ���Ϊ30Ԫ��
��2���蹺��������Ʒm������������Ʒ������80-m������
�������⣬�ã���15-10��m+��40-30����80-m����600��
��ã�m��40��
�𣺸ó�������������Ʒ40����