题目内容
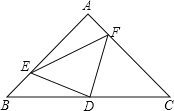
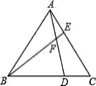
【题目】如图，已知△ABC 为等边三角形，点 D、E 分别在边 BC、AC 上，且 AE=CD，AD 与 BE相交于点 F．则∠DFE 的度数为_____°；
【答案】120
【解析】
易证△ABE≌△CAD，就可以得出∠ABE=∠CAD，由对顶角和三角形内角和可得∠DFE =∠AFB=180-（∠BAD+∠ABE）=120°．
∵△ABC为等边三角形，
∴∠BAC=∠C=60°，AB=AC．
在△ABE和△CAD中，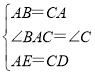
∴△ABE≌△CAD（SAS）；
∴∠ABE=∠CAD．
∴∠AFB=180-（∠BAD+∠ABE）
=180-（∠BAD+∠CAD）
=180-∠ABC
=120°
∴∠DFE =∠AFB=120°
故答案为∠DFE 的度数为120°．
练习册系列答案
相关题目
【题目】已知点A、B在数轴上分别表示a、b．
（1）对照数轴填写下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A、B两点的距离 |
（2）若A、B两点间的距离记为d，问：d和a、b有何数量关系？
（3）在数轴上标出所有符合条件的整数点，使它到5和-5的距离之和为10，并求所有这些整数的和；
（4）若点C表示的数为x，当点C在什么位置时，
取得的值最小？最小值为多少？
