题目内容
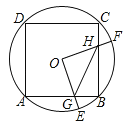
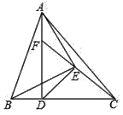
【题目】如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED, EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
A. ①③B. ①②④C. ①②③④D. ②③④
【答案】C
【解析】
①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;③证明△AEF≌△BED即可;④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
∵AD为△ABC的高线,
∴∠CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,
在△DAE和△CBE中,

∴△ADE≌△BCE(SAS);
故①正确;
②∵△ADE≌△BCE,
∴∠EDA=∠ECB,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE;
故②正确;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,
∴∠BDE=∠AFE,
∵∠BED+∠BEF=∠AEF+∠BEF=90°,
∴∠BED=∠AEF,
在△AEF和△BED中,
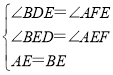
∴△AEF≌△BED(AAS),
∴BD=AF;
故③正确;
④∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故④正确;
综上①②③④都正确,故选:C.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
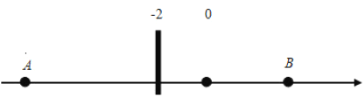
学习实践园地系列答案【题目】已知点A、B在数轴上分别表示a、b.
![]()
(1)对照数轴填写下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A、B两点的距离 |
(2)若A、B两点间的距离记为d,问:d和a、b有何数量关系?
(3)在数轴上标出所有符合条件的整数点,使它到5和-5的距离之和为10,并求所有这些整数的和;
(4)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小?最小值为多少?
取得的值最小?最小值为多少?