Question

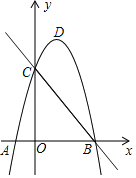
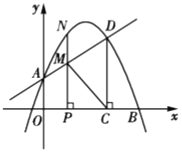
【题目】在平面直角坐标系中，抛物线y＝﹣4x2﹣8mx﹣m2+2m的顶点p．

（1）点p的坐标为　 　（含m的式子表示）

（2）当﹣1≤x≤1时，y的最大值为5，则m的值为多少；

（3）若抛物线与x轴（不包括x轴上的点）所围成的封闭区域只含有1个整数点，求m的取值范围．

Answer 1

【答案】（1）；（2）m＝1或9或﹣3；（3）或

【解析】

（1）函数的对称为：x＝﹣m，顶点p的坐标为：（﹣m，3m2+2m），即可求解；

（2）分m≤﹣1、m≥1、﹣1＜m＜1，三种情况，分别求解即可；

（3）由题意得：3m2+2m≤1，即可求解．

解：（1）函数的对称为：x＝﹣m，顶点p的坐标为：（﹣m，3m2+2m），

故答案为：（﹣m，3m2+2m）；

（2）①当m≤﹣1时，x＝1时，y＝5，即5＝﹣4﹣8m﹣m2+2m，解得：m＝﹣3；

②当m≥1时，x＝﹣1，y＝5，解得：m＝1或9；

③﹣1＜m＜1时，同理可得：m＝1或﹣（舍去）；

故m＝1或9或﹣3；

（3）函数的表达式为：y＝﹣4x2﹣8mx﹣m2+2m，

当x＝1时，y＝﹣m2﹣6m﹣4，

则1≤y＜2，且函数对称轴在y轴右侧，

则1≤﹣m2﹣6m﹣4＜2，

解得：﹣3+≤m≤﹣1；

当对称轴在y轴左侧时，1≤y＜2，

当x＝﹣1时，y＝﹣m2+10m﹣4，

则1≤y＜2，即1≤﹣m2+10m﹣4＜2，

解得：5﹣2≤m＜5﹣；

综上，﹣3+≤m≤﹣1或5﹣2≤m＜5﹣．