题目内容
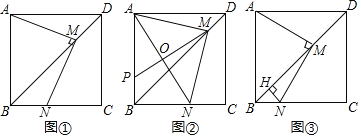
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
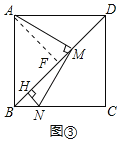
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() ;
;![]() ;(3)面积为
;(3)面积为![]() .
.
【解析】
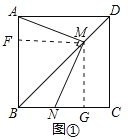
(1)过点M作MF⊥AB于F,作MG⊥BC于G,由正方形的性质得出∠ABD=∠DBC=45°,由角平分线的性质得出MF=MG,证得四边形FBGM是正方形,得出∠FMG=90°,证出∠AMF=∠NMG,证明△AMF≌△NMG,即可得出结论;
(2)证明Rt△AMN∽Rt△BCD,得出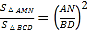 ,求出AN=2
,求出AN=2![]() ,由勾股定理得出BN=
,由勾股定理得出BN=![]() =4,由直角三角形的性质得出OM=OA=ON=
=4,由直角三角形的性质得出OM=OA=ON=![]() AN=
AN=![]() ,OM⊥AN,证明△PAO∽△NAB,得出
,OM⊥AN,证明△PAO∽△NAB,得出![]() ,求出OP=
,求出OP=![]() ,即可得出结果;
,即可得出结果;
(3)过点A作AF⊥BD于F,证明△AFM≌△MHN得出AF=MH,求出AF=![]() BD=
BD=![]() ×6
×6![]() =3
=3![]() ,得出MH=3
,得出MH=3![]() ,MN=2
,MN=2![]() ,由勾股定理得出HN=
,由勾股定理得出HN=![]() ,由三角形面积公式即可得出结果.
,由三角形面积公式即可得出结果.
(1)证明:过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,如图①所示:
,如图①所示:
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中, 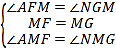
![]() ,
,
![]() ;
;
(2)解:在![]() 中,由(1)知:
中,由(1)知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
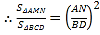
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 在
在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即:
,即: ![]() ,
,
解得:![]() ,
,
![]() ;
;
(3)解:过点![]() 作
作![]() 于
于![]() ,如图③所示:
,如图③所示:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
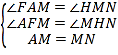
![]() ,
,
![]() ,
,
在等腰直角![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目