题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
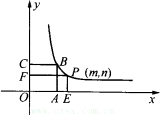
解:设点B的横坐标为a,则纵坐标为y= S正方形OABC=a· |
(2) |
解:由(1)知反比例函数的解析式为y= 故 分两种情况,当P在B点右侧时,S=9-3n= ∴n= |
(3) |
当0<m<3时,S=9-3m;当m≥3,S=9- |

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 AP,与∠DCE的平分线CF,相交于点F,连接AF,与边CD相交于点G,连接PG.
AP,与∠DCE的平分线CF,相交于点F,连接AF,与边CD相交于点G,连接PG. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. (2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn=
(2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn= (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点. (2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.
(2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.