题目内容
 (2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn=
(2013•桂林模拟)如图,已知,正方形ABCD的边长为1,以BC为对角线作第一个正方形BECO1,再以BE边为对角线作第二个正方形EFBO2,如此作下去,…则所作的第n正方形的面积Sn=| 1 |
| 2n |
| 1 |
| 2n |
分析:由正方形ABCD的边长为1,根据正方形的性质,即可求得AO1,EO2的值,则可求得S2,S3,S4的值,即可求得规律所作的第n个正方形的面积Sn.
解答:解:∵正方形ABCD的边长为1,
∴AB=1,AC=
,
∴AE=AO1=
,
∴S1=正方形BECO1=
×
=
,
同理BO2=
,
S2=
,S3=
,S4=
,
…
所作的第n正方形的面积Sn=
.
故答案为
.
∴AB=1,AC=
| 2 |
∴AE=AO1=
| ||
| 2 |
∴S1=正方形BECO1=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
同理BO2=
| 1 |
| 2 |
S2=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
…
所作的第n正方形的面积Sn=
| 1 |
| 2n |
故答案为
| 1 |
| 2n |
点评:此题考查了正方形的性质的知识点.解题的关键是熟练掌握正方形的性质以及利用找规律进行解题的方法,此题难度不大.

练习册系列答案
相关题目
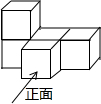 (2013•桂林模拟)如图所示的几何体的主视图是( )
(2013•桂林模拟)如图所示的几何体的主视图是( ) (2013•桂林模拟)如图,点A在双曲线y=
(2013•桂林模拟)如图,点A在双曲线y=