题目内容
如图，已知在正方形ABCD中，P为BC上的一点，E是边BC延长线上一点，连接AP过点P作PF⊥
AP，与∠DCE的平分线CF，相交于点F，连接AF，与边CD相交于点G，连接PG．（1）求证：①∠PAB=∠FPC；②AP=FP；
（2）试判断PB、DG、PC，这三条线段存在怎样的数量关系，并说明理由．
分析：（1）①根据已知条件，由同一个角的余角相等求证．
②过F作FM⊥BC交延长线于M，根据线段之间的关系，证明△ABP≌△PMF，进而求证AP=FP．
（2）过F作MN平行于CD，交CE、AD的延长线于点M、N，根据平行线的性质，结合线段之间的关系，列方程求解．
②过F作FM⊥BC交延长线于M，根据线段之间的关系，证明△ABP≌△PMF，进而求证AP=FP．
（2）过F作MN平行于CD，交CE、AD的延长线于点M、N，根据平行线的性质，结合线段之间的关系，列方程求解．
解答：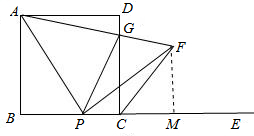
解：（1）①∵正方形ABCD，
∴∠B=90°，即∠BAP+∠APB=90°，
∵PF⊥AP，
∴∠APB+∠EPC=90°，
∴∠PAB=∠FPC．
②如图作FM⊥BC，交延长线与点M．
设AB=a，FM=b，BP=x，
则CP=a-x，
∵CF平分DCE，
∴CM=FM=b，
∴PM=a-x+b，
∵∠PAB=∠FPC，
∴△ABP∽△PMF，
∴
=
，
∴
=
，
∴
=
=1，
∴x=b，即FM=BP，
∴△ABP≌△PMF，
∴AP=FP．
（2）
=
．
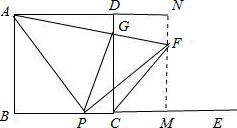
证明：如图，过F作MN平行于CD，交CE、AD的延长线于点M、N，得到矩形CMND，
即
=
，
由（1）②中得出FM=BP=CM=DN，
∵BC=MN，BP=FM，
∴PC=NF，
∴
=
．
解：（1）①∵正方形ABCD，∴∠B=90°，即∠BAP+∠APB=90°，
∵PF⊥AP，
∴∠APB+∠EPC=90°，
∴∠PAB=∠FPC．
②如图作FM⊥BC，交延长线与点M．
设AB=a，FM=b，BP=x，
则CP=a-x，
∵CF平分DCE，
∴CM=FM=b，
∴PM=a-x+b，
∵∠PAB=∠FPC，
∴△ABP∽△PMF，
∴
| AB |
| PM |
| BP |
| FM |
∴
| a |
| a-x+b |
| x |
| b |
∴
| a-x |
| a-x+b-b |
| x |
| b |
∴x=b，即FM=BP，
∴△ABP≌△PMF，
∴AP=FP．
（2）
| DG |
| PC |
| BP+PC |
| 2BP+PC |
证明：如图，过F作MN平行于CD，交CE、AD的延长线于点M、N，得到矩形CMND，
即
| DG |
| NF |
| AD |
| AN |
由（1）②中得出FM=BP=CM=DN，
∵BC=MN，BP=FM，
∴PC=NF，
∴
| DG |
| PC |
| BP+PC |
| 2BP+PC |
点评：①本题考查了正方形的性质，结合了三角形全等的判定，属于综合性比较强的题目，要求有比较扎实的基础．
②（2）涉及到探究性试题，解决本类试题要先求解，然后给出结论，再进行证明．
②（2）涉及到探究性试题，解决本类试题要先求解，然后给出结论，再进行证明．
练习册系列答案
相关题目
18、如图，已知在正方形ABCD中，P是BC上的一点，且AP=DP．求证：P是BC中点．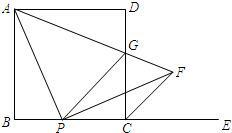
一点，连接AP．过点P作PF⊥AP，与∠DCE的平分线CF相交于点F．连接AF，与边CD相交于点G，连接PG．
如图，已知在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
（2013•仓山区模拟）如图，已知在正方形ABCD网格中，每个小方格都是边长为1的正方形，E是边DC上的一个网格的格点．
（2010•郑州模拟）如图，已知在正方形ABCD中，EF分别是AB，BC上的点，若有AE+CF=EF，请你猜想∠EDF的度数，并说明理由．