��Ŀ����
����Ŀ�������龳����ͼ�٣�P�ǡ�O���һ�㣬ֱ��PO�ֱ�O�ڵ�A��B�����Է���PA�ǵ�P����O�ϵĵ����̾��룮
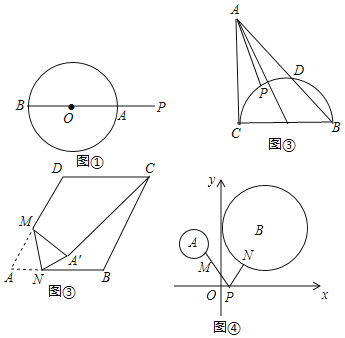
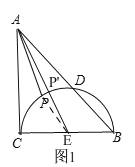
��1��ֱ�����ã���ͼ�ڣ���Rt��ABC�У���ACB��90����AC��BC��2����BCΪֱ���İ�Բ��AB��D��P�ǻ�CD�ϵ�һ�����㣬����AP����AP����Сֵ���� ����
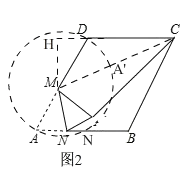
��2���������ã���ͼ�ۣ��ڱ߳�Ϊ8������ABCD�У���A��60����M��AD�ߵ��е㣬N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C�������A��C���ȵ���Сֵ��
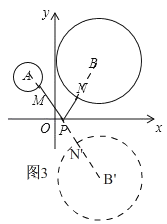
��3���ۺ����ã���ͼ�ܣ�ƽ��ֱ������ϵ�У��ֱ��Ե�A����2��3����B��3��4��ΪԲ�ģ��ֱ���1��2Ϊ�뾶����A����B��M��N�ֱ��ǡ�A����B�ϵĶ��㣬PΪx���ϵĶ��㣬��PM+PN����Сֵ������ ����
���𰸡���1��![]() ��1����2��4
��1����2��4![]() ��4����3��
��4����3��![]() ��3
��3
��������
��1����ȷ����AP��Сʱ��P��λ�ã���ͼ1�е�P'��λ�ã����ɵó����ۣ�
��2�����жϳ�A'M��AM��MD���ٹ����ֱ�������Σ�����������Ǻ������DH��MH���������ù��ɶ������CM�����ɵó����ۣ�
��3�����öԳ���ȷ������B����x��ĶԳƵ�B'�������������.
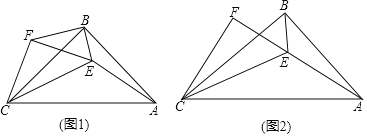
��1����ͼ1��ȡBC���е�E��
����AE������Բ��P'���ڰ�Բ��ȡһ��P������AP��EP��
����AEP��AP+EP��AE��
����AP'��AP����Сֵ��
��AE��![]() ��P'E��1��
��P'E��1��
��AP'��![]() ��1��
��1��
�ʴ�Ϊ��![]() ��1��
��1��
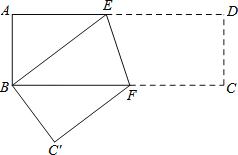
��2����ͼ2�����۵�֪��A'M��AM��
��M��AD���е㣬
��A'M��AM��MD��
���Ե�A'����ADΪֱ����Բ�ϣ�
������A'��CM��ʱ��A'C�ij���ȡ����Сֵ��
����M��MH��CD��H��
��Rt��MDH��DH��DMcos��HDM��2��MH��DMsin��HDM��2![]() ��
��
��Rt��CHM��CM��![]() ��4
��4![]() ��
��
��A'C��CM��A'M��4![]() ��4��
��4��
��3����ͼ3������B����x��ĶԳ�Բ��B'������AB'��x����P��
��B��3��4����
��B'��3����4����
��A����2��3����
��AB'��![]() ��
��![]()
��PM+PN����Сֵ��AB'��AM��B'N'��AB'��AM��BN��![]() ��3.
��3.
�ʴ�Ϊ��![]() ��3.
��3.