题目内容

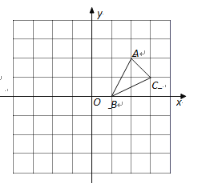
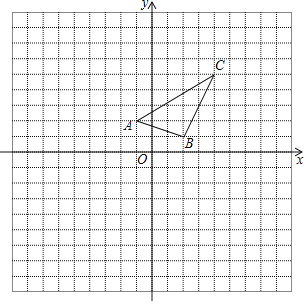
【题目】如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．

（1）以原点O为位似中心，在x轴的上方画出△A1B1C1，使△A1B1C1与△ABC位似，且相似比为2；

（2）△A1B1C1的面积是　 　平方单位．

（3）点P（a，b）为△ABC内一点，则在△A1B1C1内的对应点P’的坐标为　 　．

【答案】（1）见解析；（2）28；（3）（2a，2b）．

【解析】

（1）连接OB，延长OB到B1使得OB1=2OB，同法作出A1，C1，连接A1C1，B1C1，A1B1即可．

（2）两条分割法求出三角形的面积即可．

（3）利用相似三角形的性质解决问题即可．

解：（1）△A1B1C1即为所求．

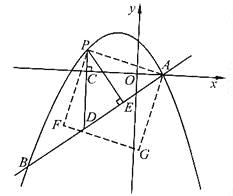
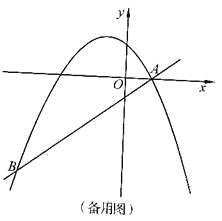
（2）△A1B1C1的面积＝4S△ABC＝4×（4×5﹣×3×5﹣×1×3﹣×2×4）＝28，

故答案为：28．

（3）点P（a，b）为△ABC内一点，则在△A1B1C1内的对应点P’的坐标为（2a，2b），

故答案为：（2a，2b）．

练习册系列答案
相关题目

【题目】问题情境：如图①，P是⊙O外的一点，直线PO分别交⊙O于点A、B，可以发现PA是点P到⊙O上的点的最短距离．

（1）直接运用：如图②，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是　 　．

（2）构造运用：如图③，在边长为8的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，请求出A′C长度的最小值．

（3）综合运用：如图④，平面直角坐标系中，分别以点A（﹣2，3），B（3，4）为圆心，分别以1、2为半径作⊙A、⊙B，M、N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值等于　 　．

【题目】如图，△ABC是一块等边三角形的废铁片，其中AB=AC=10，BC=12．利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F． G分别落在AC、AB上．

（1）小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了．请你帮小聪求出正方形的边长．

（2）小明想：不求正方形的边长也能画出正方形．具体作法是：

①在AB边上任取一点G′，如图2作正方形G′D′E′F′；

②连接BF′并延长交AC于点F；

③过点F作FE∥F′E′交BC于点E，FG∥F′G′交AB于点G，GD∥G′D′交BC于点D，则四边形DEFG即为所求的正方形．你认为小明的作法正确吗？说明理由．

【题目】如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8.

（1）求该抛物线的解析式；

（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.

①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；

②连接PA，以PA为边作图示一侧的正方形APFG.随着点P的运动，正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标.

【题目】关公，作为运城乃至山西的一张名片，吸引了来自世界各地的游客，在运城西南公里的常平村(关公故乡)南山上，有一尊巨型关公铜像，高米，象征关公享年岁，底座的高度也有一定寓意．有一位游客，对此产生了兴趣，想测量它的高度，由于游客无法直接到达铜像底部，因此该游客计划借助坡面高度来测量它的高度.如图，代表底座的高，坡顶与底座底部处在同一水平面上，该游客在斜坡底处测得该底座顶端的仰角为，然后他沿着坡度为的斜坡攀行了米，在坡顶处又测得该底座顶端的仰角为．求：

坡顶到地面的距离；

求底座的高度(结果精确到米)．

(参考数据:，

【题目】如图，在平面直角坐标系中，点 A 和点 C 分别在x 轴和 y 轴的正半轴上，OA=6，OC=4，以 OA，OC 为邻边作矩形 OABC， 动点 M，N 以每秒 1 个单位长度的速度分别从点 A、C 同时出发，其中点 M 沿 AO 向终点 O 运动，点 N沿 CB 向终点 B 运动，当两个动点运动了 t 秒时，过点 N 作NP⊥BC，交 OB 于点 P，连接 MP．

（1）直接写出点 B 的坐标为 ，直线 OB 的函数表达式为 ;

（2）记△OMP 的面积为 S，求 S 与 t 的函数关系式；并求 t 为何值时，S有最大值，并求出最大值．

【题目】如图，△ABC的顶点的坐标分别为A(2，2)，B(1，0)，C(3，1)

(1)画出△ABC关于x轴对称的；

(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2，写出点C2的坐标；

(3)在(1)(2)的基础上，图中的，关于哪个点中心对称．

【题目】文化是一个国家、一个民族的灵魂，近年来，央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目．为了解学生对这些栏目的喜爱情况，某学校组织学生会成员随机抽取了部分学生进行调查，被调查的学生必须从《经曲咏流传》（记为A）、《中国诗词大会》（记为B）、《中国成语大会》（记为C）、《朗读者》（记为D）中选择自己最喜爱的一个栏目，也可以写出一个自己喜爱的其他文化栏目（记为E）．根据调查结果绘制成如图所示的两幅不完整的统计图．

请根据图中信息解答下列问题：

（1）在这项调查中，共调查了多少名学生？

（2）将条形统计图补充完整，并求出扇形统计图中“B”所在扇形圆心角的度数；

（3）若选择“E”的学生中有2名女生，其余为男生，现从选择“E”的学生中随机选出两名学生参加座谈，请用列表法或画树状图的方法求出刚好选到同性别学生的概率．

【题目】如图，已知等腰直角，点是斜边上一点(不与重合)，是的外接圆的直径．

（1）求证：是等腰直角三角形；

（2）若的直径为2，求的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网