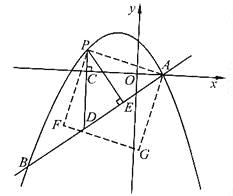
题目内容
【题目】已知二次函数f（x）＝ax2+bx+c和一次函数g（x）＝﹣bx，其中a、b、c，满足a＞b＞c，a+b+c＝0．
（1）求证：这两个函数的图象交于不同的两点；
（2）设这两个函数的图象交于A，B两点，作AA1⊥x轴于A1，BB1⊥x轴于B1，求线段A1B1的长的取值范围．
【答案】（1）见解析；（2）
＜A1B1＜2．
【解析】
（1）把两个函数联立成方程组，转化为解一元二次方程，用根的判别式求解即可；
（2）A1B12＝（x1﹣x2）2＝（x1+x2）2﹣4x1x2，用根与系数的关系转化为含a、b、c的式子，再配方求解.
（1）证明：联立方程得：ax2+2bx+c＝0，
△＝4（b2-ac），
∵a＞b＞c，a+b+c＝0，
∴a＞0，c＜0，
∴ac＜0，
∴△＞0，
∴两函数的图象相交于不同的两点；
（2）解：设方程ax2+2bx+c＝0的两根为x1，x2，则
A1B12＝（x1﹣x2）2＝（x1+x2）2﹣4x1x2，
＝（﹣
）2﹣
＝
＝
，
＝4[（
）2++1]，
＝4[（
）2+
]，
∵a＞b＞c，a+b+c＝0，
∴b＝﹣（a+c）,
∴a＞﹣（a+c）＞c，a＞0，
∴﹣2＜＜﹣
，
此时3＜A1B12＜12，
∴＜A1B1＜2．
【题目】某商店销售一种商品，经市场调査发现，该商品的周销售量y（件）是售价x（元/件）的一次函数．其售价、周销售量、周销售利润w（元）的三组对应值如表：
售价x（元/件） | 50 | 60 | 80 |
周销售量y（件） | 100 | 80 | 40 |
周销售利润w（元） | 1000 | 1600 | 1600 |
注：周销售利润＝周销售量×（售价﹣进价）
（1）求y关于x的函数解析式_____；
（2）当售价是_____元/件时，周销售利润最大．
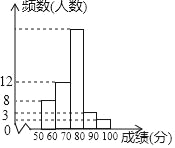
【题目】（7分）某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：
成绩分组 | 频数 | 频率 |
50≤x＜60 | 8 | 0.16 |
60≤x＜70 | 12 | a |
70≤x＜80 | ■ | 0.5 |
80≤x＜90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
（1）写出a，b，c的值；
（2）请估计这1000名学生中有多少人的竞赛成绩不低于70分；
（3）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率．
