题目内容
【题目】如图，在矩形纸片ABCD中，AB＝4cm，AD＝8cm，按如图方式折叠，使点D与点B重合，折痕为EF，则tan∠BEF＝（ ）
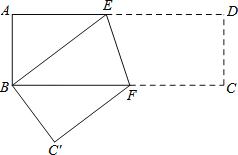
A.2B.3C.4D.5
【答案】A
【解析】
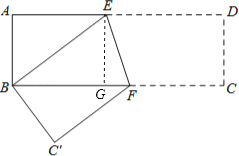
过点E作EG⊥BC于点G，在直角△ABE中，根据勾股定理求出AE，BE，再求出BG、GF，进而即可求解．
如图，过点E作EG⊥BC于点G，
∵四边形ABCD为矩形，
∴∠A＝∠C＝90°，BC＝AD＝8cm，AB＝DC＝4cm，
设BE＝DE=λ，CF＝C′F=μ，
则AE＝8﹣λ，BF＝8﹣μ；在直角△ABE中，
由勾股定理得：λ2＝（8﹣λ）2+42，
解得：λ＝5，
∴AE＝8﹣5＝3cm，
在直角△BFC′中，同理可求：μ＝3，
∴BF＝8﹣3＝5cm，
∵BG＝AE＝3cm，
∴GF＝5﹣3＝2cm；
∵GE＝AB＝4cm，
∴tan∠EFG＝
,
∵∠BEF＝∠DEF，ED∥CF，
∴∠EFG＝∠DEF=∠BEF，
∴tan∠BEF＝2．
故选：A．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
