题目内容
【题目】已知,在△ABC和△EFC中,∠ABC=∠EFC=90°,点E在△ABC内,且∠CAE+∠CBE=90°
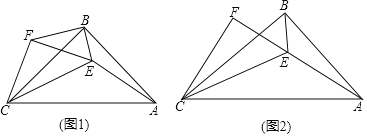
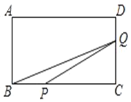
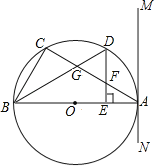
(1)如图1,当△ABC和△EFC均为等腰直角三角形时,连接BF,
①求证:△CAE∽△CBF;
②若BE=2,AE=4,求EF的长;
(2)如图2,当△ABC和△EFC均为一般直角三角形时,若![]() =k,BE=1,AE=3,CE=4,求k的值.
=k,BE=1,AE=3,CE=4,求k的值.
【答案】(1)①见解析;②2![]() ;(2)
;(2)![]()
【解析】
(1)①先判断出∠BCF=∠ACE,再判断出![]() ,即可得出结论;
,即可得出结论;
②先判断出∠CBF=∠CAE,进而判断出∠EBF=90°,再求出BF=2![]() ,最后用勾股定理求解即可得出结论;
,最后用勾股定理求解即可得出结论;
(2)先判断出∠BCF=∠ACE,再判断出![]() ,进而判断出△BCF∽△ACE,进而表示出BF=
,进而判断出△BCF∽△ACE,进而表示出BF=![]() ,再表示出EF=
,再表示出EF=![]() ,最后用勾股定理得,BE2+BF2=EF2,建立方程求解即可得出结论.
,最后用勾股定理得,BE2+BF2=EF2,建立方程求解即可得出结论.
解:(1)①∵△ABC和△CEF都是等腰直角三角形,
∴∠ECF=∠ACB=45°,
∴∠BCF=∠ACE,
∵△ABC和△CEF都是等腰直角三角形,
∴CE=![]() CF,AC=
CF,AC=![]() CB,
CB,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴△BCF∽△ACE;
②由①知,△BCF∽△ACE,
∴∠CBF=∠CAE,![]() =
=![]() ,
,
∴BF=![]() AE=
AE=![]() ×4=
×4=![]() ,
,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
即:∠EBF=90°,
根据勾股定理得,EF=![]() ;
;
(2)如图(2),连接BF,
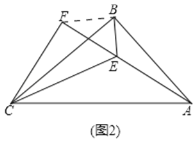
在Rt△ABC中,tan∠ACB=![]() =k,
=k,
同理,tan∠ECF=k,
∴tan∠ACB=tan∠ECF,
∴∠ACB=∠ECF,
∴∠BCF=∠ACE,
在Rt△ABC中,设BC=m,则AB=km,
根据勾股定理得,AC=![]() ;
;
在Rt△CEF中,设CF=n,则EF=nk,同理,CE=![]() ,
,
∴![]() ,
, ,
,
∴![]() ,
,
∵∠BCF=∠ACE,
∴△BCF∽△ACE,
∴∠CBF=∠CAE,
∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
即:∠EBF=90°,
∵△BCF∽△ACE,
∴![]()
∴BF=![]() AE=
AE=![]()
∵CE=4,
∴![]() ,
,
∴n=![]() ,
,
∴EF=![]() ,
,
在Rt△EBF中,根据勾股定理得,BE2+BF2=EF2,
∴12+(![]() )2=(
)2=(![]() )2,
)2,
∴k=![]() 或k=
或k=![]() (舍),
(舍),
即:k的值为![]() .
.

 名校课堂系列答案
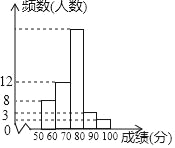
名校课堂系列答案【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.