题目内容
【题目】某产品每件成本28元，在试销阶段产品的日销售量y（件）与每件产品的日销售价x（元）之间的关系如图中的折线所示．为维持市场物价平衡，最高售价不得高出83元．
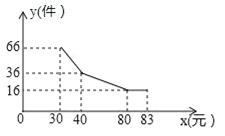
（1）求y与x之间的函数关系式；
（2）要使每日的销售利润w最大，每件产品的日销售价应定为多少元？此时每日销售利润是多少元？
【答案】（1）y与x之间的函数关系式是：
y=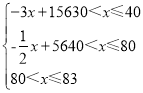
；
（2）每件产品的日销售价应定为70元，此时每日销售利润是882元．
【解析】
试题分析：（1）根据函数图象可知该函数分为三段，然后分别设出相应的函数解析式，根据图象提供的信息求出相应的函数解析式即可解答本题；
（2）根据第（1）问中的函数解析式可以求出所对应的利润，然后求出各段的最大利润然后进行比较即可解答本题．
试题解析：（1）当30＜x≤40时，设此段的函数解析式为：y=kx+b，
解得，k=﹣3，b=156
∴当30＜x≤40时，函数的解析式为：y=﹣3x+156；
当40＜x≤80时，设此段函数的解析式为：y=mx+n，
解得，m=
，n=56，
∴当40＜x≤80时，函数的解析式为：y=
；
当80＜x≤83时，y=16；
由上可得，y与x之间的函数关系式是：y=；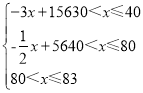
（2）当30＜x≤40时，
w=（x﹣28）y
=（x﹣28）（﹣3x+156）
=﹣3x2+240x﹣4368
=﹣3（x﹣40）2+432
∴当x=40时取得最大值，最大值为w=432元；
当40＜x≤80时，
w=（x﹣28）y
=（x﹣28）（）
=
∴当x=70时，取得最大值，最大值为w=882元；
当80＜x≤83时，w=（x﹣28）×16
∴当x=83时，取得最大值，最大值为w=880元；
由上可得，当x=70时，每日点的销售利润最大，最大为882元，
即要使每日的销售利润w最大，每件产品的日销售价应定为70元，此时每日销售利润是882元．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
