Question

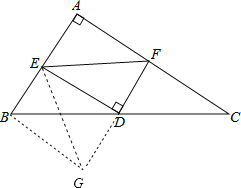
【题目】△ABC中，∠A＝90°，D是BC的中点，E、F分别在AB、AC上，且DE⊥DF，BE＝2，CF＝4，则EF的长为_____．

Answer 1

【答案】2．

【解析】

延长FD至点G，使得DG＝DF，连接BG，EG，易证△CDF≌△BDG，可得BG＝CF＝4，∠C＝∠DBG，可证明∠ABG＝90°，再根据等腰三角形底边三线合一性质可得EF＝EG，即可求得EF的长，即可解题．

延长FD至点G，使得DG＝DF，连接BG，EG，

∵在△CDF和△BDG中，

，

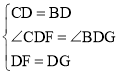∴△CDF≌△BDG（SAS），

∴BG＝CF＝4，∠C＝∠DBG，

∵∠C+∠ABC＝90°，

∴∠DBG+∠ABC＝90°，即∠ABG＝90°，

∵DE⊥FG，DF＝DG，

∴EF＝EG＝．

故答案为：2