题目内容
【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
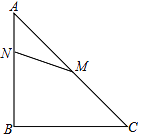
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
【答案】(1)见解析;(2)y=![]() (x﹣3)2+
(x﹣3)2+ ![]() ,最小值为
,最小值为![]() .
.
【解析】
(1)根据旋转的定义,画出旋转90°的△A1PM即可;
(2)过点M作MD⊥AB于点D,用割补法表示出四边形NMCP的面积y,化为顶点式,根据二次函数的性质求解即可.
(1)解:如图所示:△A1PM,即为所求;
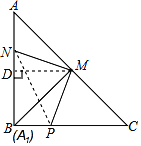
(2)解:过点M作MD⊥AB于点D,
∵AB=BC=4,∠ABC=90°,M是AC的中点,
∴MD=2,
设AN=x,则BN=4﹣x,
故四边形NMCP的面积为:
y= ![]() ×4×4﹣
×4×4﹣ ![]() x×2﹣
x×2﹣ ![]() x×(4﹣x)
x×(4﹣x)
= ![]() x2﹣3x+8
x2﹣3x+8
= ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
故y的最小值为: ![]()

练习册系列答案
相关题目