题目内容
【题目】如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
(1)求点B、点D的坐标,
(2)判断△ACD的形状,并求出△ACD的面积.

【答案】(1)B点坐标为(﹣1,0),D点坐标为(0,3);(2)△ACD是以AC为斜边的直角三角形,面积为3.
【解析】
(1)由顶点坐标和A点坐标,可求得抛物线的解析式,容易求出B、D的坐标;
(2)根据点的坐标,利用勾股定理可求得AD、AC、CD的长,可判断△ACD的形状.
解:(1)∵抛物线的顶点坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵与x轴交于点A(3,0),
∴0=4a+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3,
令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,令x=0,可得y=3
∴B点坐标为(﹣1,0),D点坐标为(0,3);
(2)∵A(3,0),D(0,3),C(1,4),
∴AD=![]() =3
=3![]() ,CD=
,CD=![]() =
=![]() ,AC=
,AC=![]() =2
=2![]() ,
,
∴AD2+CD2=(3![]() )2+(
)2+(![]() )2=20=(2
)2=20=(2![]() )2=AC2 ,
)2=AC2 ,
∴△ACD是以AC为斜边的直角三角形,
∴S△ACD=![]() ADCD=
ADCD=![]() ×3
×3![]() ×
×![]() =3.
=3.

 浙江名校名师金卷系列答案
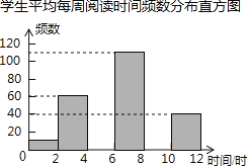
浙江名校名师金卷系列答案【题目】为引导学生广泛阅读古今文学名著,某校开展了读书活动.学生会随机调查了部分学生平均每周阅读时间的情况,整理并绘制了如下的统计图表:
学生平均每周阅读时间频数分布表
平均每周阅读时间x(时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | b |
8≤x<10 | 100 | 0.250 |
10≤x≤12 | 40 | 0.100 |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题;
(1)在频数分布表中,a=______,b=______;
(2)补全频数分布直方图;
(3)如果该校有1600名学生,请你估计该校平均每周阅读时间不少于6小时的学生大约有多少人?