题目内容
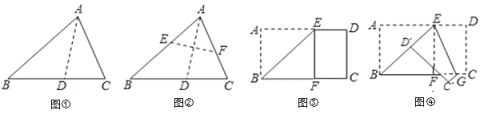
【题目】![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,点
,点![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 延长交
延长交![]() 于
于![]() ,
,![]() .小华得出
.小华得出![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() .
.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
【答案】D
【解析】
首先连接OE,CE,由OE=OD,PE=PF,易得∠OED+∠PEF=∠ODE+∠PFE,又由OD⊥BC,可得OE⊥PE,继而证得PE为⊙O的切线;
又由BC是直径,可得CE⊥AB,由切线长定理可得GC=GE,根据等角的余角相等,可得∠A=∠AEG,根据等腰三角形的判定,可得答案;
易证得OG是△ABC的中位线,则可得OG∥BE.
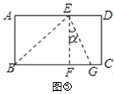
连接OE,CE.
∵OE=OD,PE=PF,∴∠OED=∠ODE,∠PEF=∠PFE.
∵OD⊥BC,∴∠ODE+∠OFD=90°.
∵∠OFD=∠PFE,∴∠OED+∠PEF=90°,即OE⊥PE.
∵点E在⊙O上,∴GE为⊙O的切线;
点C在⊙O上,OC⊥GC,∴GC为⊙O的切线,∴GC=GE.
故①正确;
∵BC是直径,∴∠BEC=90°,∴∠AEC=90°.
∵∠ACB=90°,∴AC是⊙O的切线,∴EG=CG,∴∠GCE=∠GEC.
∵∠GCE+∠A=90°,∠GEC+∠AEG=90°,∴∠A=∠AEG,∴AG=EG;故②正确;
∵OC=OB,AG=CG,∴OG是△ABC的中位线,∴OG∥AB;故③正确.
故选D.

练习册系列答案
相关题目