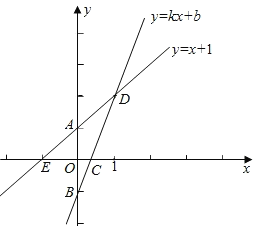��Ŀ����
����Ŀ��(1)�۲��뷢�֣�С����������ֽƬ![]() �ع���
�ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() ����,�ۺ�Ϊ
����,�ۺ�Ϊ![]() ,չ��ֽƬ(��ͼ��);�ڵ�һ�ε��۵������ϵڶ����۵���������ֽƬ,ʹ��
,չ��ֽƬ(��ͼ��);�ڵ�һ�ε��۵������ϵڶ����۵���������ֽƬ,ʹ��![]() �͵�
�͵�![]() �غ�,�ۺ�Ϊ
�غ�,�ۺ�Ϊ![]() ,չƽֽƬ��õ�
,չƽֽƬ��õ�![]() (��ͼ��).С����Ϊ
(��ͼ��).С����Ϊ![]() �ǵ��������Σ���ͬ����?��˵������.
�ǵ��������Σ���ͬ����?��˵������.
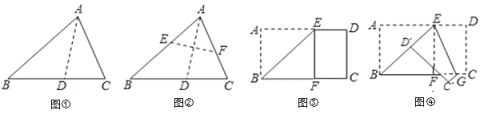
(2)ʵ�������ã�������ֽƬ![]() �ع���
�ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() ���ϵĵ�
���ϵĵ�![]() ��,�ۺ�Ϊ
��,�ۺ�Ϊ![]() (��ͼ��);���ع���
(��ͼ��);���ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() �ϵĵ�
�ϵĵ�![]() ��,�ۺ�Ϊ
��,�ۺ�Ϊ![]() (��ͼ��);��չƽֽƬ(��ͼ��).��ͼ����
(��ͼ��);��չƽֽƬ(��ͼ��).��ͼ����![]() �Ĵ�С��
�Ĵ�С��
���𰸡�(1)ͬ��.���ɼ�������(2) ![]() .
.
��������
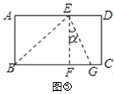
��1���������۵�֪����A��EF���д����ϣ�����AE=AF��
��2����ͼ֪������=��FED����180�㩁��AEB����2��
��1��ͬ�⣮��ͼ����AD��EF���ڵ�G��
���۵�֪��ADƽ�֡�BAC�����ԡ�BAD=��CAD��
�����۵�֪����AGE=��DGE����AGE+��DGE=180�㣬
���ԡ�AGE=��AGF=90�㣬
���ԡ�AEF=��AFE������AE=AF��
����AEF����������
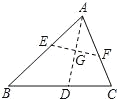
��2�����۵�֪���ı���ABFE�������Σ���AEB=45�㣬
���ԡ�BED=135�ȣ�
�����۵�֪����BEG=��DEG��
���ԡ�DEG=67.5�ȣ�
�Ӷ�����=67.5�㩁45��=22.5�㣮

��ϰ��ϵ�д�
 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
�����Ŀ