题目内容
【题目】已知:如图,直线y=﹣x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=![]() 的图象上.
的图象上.
(1)求点A与B的坐标;
(2)求k的值;
(3)若y轴正半轴有点P,过点P作x轴的平行线,且与反比例函数y=![]() 的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=
的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=![]() S△OAB时,求点P的坐标.
S△OAB时,求点P的坐标.

【答案】(1)A(3,0),B(0,3);(2)k的值为9;(3)P(0,2)或(0,6)
【解析】
(1)设A(a,0);B(0,b)代入即可求出a、b的值.进而求出A、B坐标.(2)如图① ,根据点O与O′关于直线AB对称,可知四边形OAO′B为正方形即可得答案.(3)设P(0,m),分两种情况:①当点P在点B的上方时,即:m>3,延长AO′于PQ相交于点M,设P(0,m),由面积关系可求;②当点P在点B的下方时,即:0<m<3,方法同上.
(1)设A(a,0);B(0,b),代入y=﹣x+3得:a=3,b=3,
所以A(3,0);B(0,3).
(2)如图①
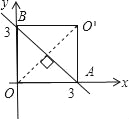
图①
∵点O与O′关于直线AB对称,
∴由题意可得四边形OAO′B为正方形,
∴O′(3,3)
则 k=3×3=9
即:k的值为9
(3)设P(0,m),显然,点P与点B不重合
①当点P在点B的上方时,即:m>3,
延长AO′于PQ相交于点M,如图②所示:

则:Q(![]() ,m),M(3,m)
,m),M(3,m)
∴PM=3,AM=m,MO′=m﹣3,QM=3﹣![]() ,
,
∴S=S△PMA﹣S△QMO′=![]() =
=![]() ×
×![]() =
=![]()
∴![]() ﹣
﹣![]() (3﹣m)(m+3)=
(3﹣m)(m+3)=![]() ,
,
解之得:m=6
②当点P在点B的下方时,即:0<m<3,如图③所示:
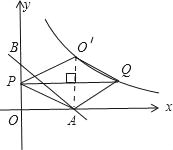
显然,PQ⊥AO′,
∴S=![]() PQAO′=
PQAO′=![]() ×3×
×3×![]() =
=![]() ,
,
∴m=2
∴P(0,2)或(0,6).

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目