题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=90°.
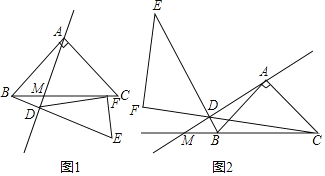
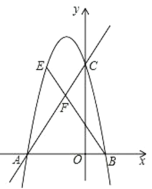
(1)如图1,若直线AD与BC相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD于F,证明:AD=EF+BD.
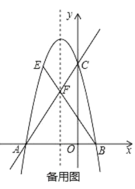
(2)如图2,若直线AD与CB的延长线相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD交CD的延长线于F,探究:AD、EF、BD之间的数量关系,并证明.
【答案】(1)见解析;(2)AD+BD=EF,理由见解析.
【解析】
(1)将△ABD绕点A逆时针方向旋转90°至△ACG,得到BD=CG,延长GC交DE于点H,证明四边形ADHG为正方形,则AD=GH,证明△DEF≌△DCH,得到EF=CH,则得出结论;
(2)作CN⊥AM,证明△DEF≌△CDN,得到EF=DN,证明△ADB≌△CNA.得到BD=AN.则AD+AN=DN=EF.
证明:(1)∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
如图1,将△ABD绕点A逆时针方向旋转90°至△ACG,
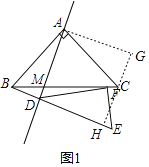
∴BD=CG,
延长GC交DE于点H,
∵AD⊥BE,∠DAG=∠AGC=90°,AD=AG,
∴四边形ADHG为正方形,
∴∠DHC=90°,
∴AD=GH,
∵DE=DC,EF⊥CD,∠EDF=∠CDH,
∴△DEF≌△DCH(AAS),
∴EF=CH,
∴AD=GH=GC+CH=EF+BD;
(2)AD+BD=EF,理由如下:
作CN⊥AM,

∵AD⊥BE,
∴∠EDF+∠ADC=90°,
∵∠DCN+∠ADC=90°,
∴∠EDF=∠DCN,
∵∠F=∠DNC=90°,DE=DC,
∴△DEF≌△CDN(AAS),
∴EF=DN,
∵∠BAC=90°,
∴∠DAB+∠NAC=90°,
又∵∠DAB+∠DBA=90°,
∴∠NAC=∠DBA,
∵AB=AC,
∴△ADB≌△CNA(AAS).
∴BD=AN.
∴AD+AN=DN=EF,
∴AD+BD=EF.

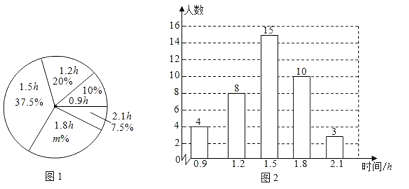
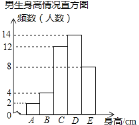
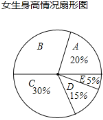
【题目】某校为了了解学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成下面的统计图表:
组别 | A | B | C | D | E |
身高(cm) | x<150 | 150≤x<155 | 155≤x<160 | 160≤x<165 | x≥165 |
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
(3)从男生样本的A、B两组里,随机安排2人参加一项活动,求恰好是1人在A组、1人在B组的概率.
【题目】生物学上研究表明:不同浓度的生长素对植物的生长速度影响不同,在一定范围内,生长素的浓度对植物的生长速度有促进作用,相反,在某些浓度范围,生长速度会变缓慢,甚至阻碍植物生长(阻碍即植物不生长,甚至枯萎).小林同学在了解到这一信息后,决定研究生长素浓度与茶树生长速度的关系,设生长素浓度为x克/升,生长速度为y毫米/天,当x超过4时,茶树的生长速度y与生长素x浓度满足关系式:![]() .实验数据如下表,当生长速度为0时,实验结束.
.实验数据如下表,当生长速度为0时,实验结束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如图,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,画出该函数图象;
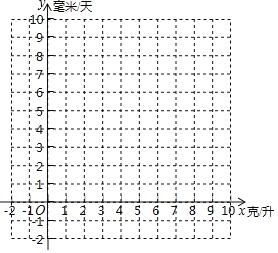
(2)根据上述表格,求出整个实验过程中y与x的函数关系式,并写出自变量x的取值范围;
(3)结合画出的函数图象,写出该函数的一条性质: ;
(4)若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是: .