题目内容
【题目】生物学上研究表明:不同浓度的生长素对植物的生长速度影响不同,在一定范围内,生长素的浓度对植物的生长速度有促进作用,相反,在某些浓度范围,生长速度会变缓慢,甚至阻碍植物生长(阻碍即植物不生长,甚至枯萎).小林同学在了解到这一信息后,决定研究生长素浓度与茶树生长速度的关系,设生长素浓度为x克/升,生长速度为y毫米/天,当x超过4时,茶树的生长速度y与生长素x浓度满足关系式:![]() .实验数据如下表,当生长速度为0时,实验结束.
.实验数据如下表,当生长速度为0时,实验结束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如图,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,画出该函数图象;
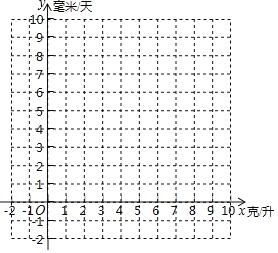
(2)根据上述表格,求出整个实验过程中y与x的函数关系式,并写出自变量x的取值范围;
(3)结合画出的函数图象,写出该函数的一条性质: ;
(4)若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是: .
【答案】(1)画出该函数图象如图所示;见解析;(2)
(3)当0<x<4时,y随x的增大而增大;(4)![]() .
.
【解析】
(1)把表中的x,y的值分别描入平面直角坐标系中,再用直线或平滑的曲线连接即可;
(2)利用待定系数法进行求解,当0<x<4时,函数图像是直线,当4≤x≤8时,函数图像是抛物线;
(3)当0<x<4时,函数图像是直线,![]() ,y随x的增大而增大;
,y随x的增大而增大;
(4)直线y=kx+3过点(0,3),要与上述函数图像有2个交点,则直线过点(4,10)或(8,0),代入求解出k的值,进而求出k的取值范围.
(1)画出该函数图象如图所示;
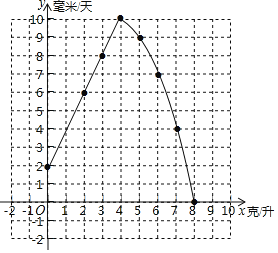
(2)当0<x<4时,设y=kx+b,
把(0,2),(2,6)代入y=kx+b得,![]() ,
,
解得:![]() ,
,
∴y=2x+2;
当4≤x≤8时,
把(7,4),(8,0)代入![]() 得,
得,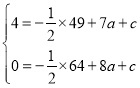
解得:![]()
∴y=﹣![]() x2+
x2+![]() x+4;
x+4;
∴整个实验过程中y与x的函数关系式为: ;
;
(3)当0<x<4时,y随x的增大而增大,
故答案为:当0<x<4时,y随x的增大而增大;
(4)∵直线y=kx+3与上述函数图象有2个交点,
∴当直线y=kx+3过(4,10)或(8,0)时,
即把(4,10)或(8,0)分别代入y=kx+3得,k=![]() 或k=﹣
或k=﹣![]() ,
,
∴若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是:![]()
故答案为:![]() .
.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案