题目内容
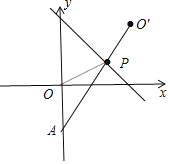
【题目】在平面直角坐标系中,点O为坐标原点,点A(0,﹣2),抛物线y=![]() ﹣2x+2的顶点为P,AP+OP的最小值为______.
﹣2x+2的顶点为P,AP+OP的最小值为______.
【答案】2![]()
【解析】
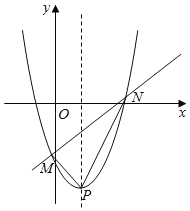
利用配方法得到P(m,2﹣m),则可判断点P在直线y=﹣x+2上,作出点O(0,0)关于直线y=﹣x+2的对称点O′,则O′的坐标为(2,2),连接O′A交直线y=﹣x+2于P,如图,利用两点之间线段最短可判断此时PA+PO的值最小,然后计算出O′A即可.
∵抛物线y=![]() ﹣2x+2=
﹣2x+2=![]() (x﹣m)2+2﹣m,
(x﹣m)2+2﹣m,
∴P(m,2﹣m),
∴点P在直线y=﹣x+2上,
点O(0,0)关于直线y=﹣x+2的对称点O′的坐标为(2,2),
连接O′A交直线y=﹣x+2于P,如图,
∴PA+PO=PA+PO′=O′A,此时PA+PO的值最小,
∵点A(0,﹣2),
∴O′A=![]() =2
=2![]() ,
,
∴AP+OP的最小值为2![]() .
.
故答案为2![]() .
.

练习册系列答案
相关题目