Question

【题目】如图，在Rt△ABC中，∠C=90°，CD⊥AB，BE平分∠ABC交CD于F，EH⊥CD于H，则下列结论：①；②；③；④若F为BE中点，则AD=3BD，其中正确的结论有( )

A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

①证明△ACD∽△CBD即可作出判断；

②根据勾股定理即可得解；

③作EM⊥AB，可证△BCE≌△BEM，从而得到为定值，依此即可作出判断；

④若F为BE中点，则CF=EF=BF，可得∠BCD=∠CBF=∠DBF=30°，再根据含30°的直角三角形的性质即可作出判断．

∵CD⊥AB，

∴∠CDA=∠CDB，∠A+∠ACD=90°, ∠CBD+∠BCD=90°，

∵∠ACB=90°,

∴∠ACD+∠BCD=90°,

∴∠A=∠BCD

∴△ACD∽△CBD

∴

∴

故①正确；

∵AC2-AD2=BC2-BD2=CD2，

∴AC2+BD2=BC2+AD2，

故②正确；

作EM⊥AB，则BD+EH=BM，

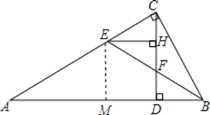
∵BE平分∠ABC，△BCE≌△BEM，

∴BC=BM=BD+EH，

∴=1，故③正确；

∵F为BE中点，

∴BF=EF，

∵BE是∠ABC的平分线，

∴∠ABE=∠CBE，

∴∠BFD=90°-∠DBF，

∴∠CFE=90°-∠DBF，

又∠CEF=∠A+∠ABE=90°-∠ABC+∠ABE=90°-∠ABE，

∴∠CFE=∠CEF

∴CE=CF

∵F为BE中点

∴CF=CE

∴CF=EF=BF，

∴∠BCD=∠CBF=∠DBF=30°，∠A=30°，

∴AB=2BC=4BD，

∴AD=3BD，故④正确．

∴正确的结论有4个.

故选D．