题目内容
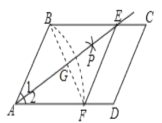
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B. F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,AG=2![]() ,则四边形ABEF的面积是( )
,则四边形ABEF的面积是( )
A.8![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由作法得AE平分∠BAD,AB=AF,所以∠1=∠2,再证明AF=BE,则可判断四边形AFEB为平行四边形,于是利用AB=AF可判断四边形ABEF是菱形;根据菱形的性质得BF⊥AE,AG=EG,求出BF和AE的长,即可得出结果.
由作法得AE平分∠BAD,AB=AF,
则∠1=∠2,
∵四边形ABCD为平行四边形,
∴BE∥AF,∠BAF=∠C=60°,
∴∠2=∠BEA,
∴∠1=∠BEA=30°,
∴BA=BE,
∴AF=BE,
∴四边形AFEB为平行四边形,△ABF是等边三角形,而AB=AF,
∴四边形ABEF是菱形;
∴BF⊥AE,AG=EG,
∵四边形ABEF的周长为16,
∴AF=BF=AB=4,
在Rt△ABG中,∠1=30°,
∵AG=2![]() ,
,
∴AE=2AG=4![]() ,
,
∴菱形ABEF的面积=![]() BF×AE=
BF×AE=![]() ×4×4
×4×4![]() =8
=8![]() ;
;
故答案为:A.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目