题目内容
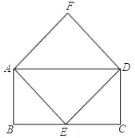
【题目】正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝kx+b和x轴上，已知点B1（1，1），B2（3，2），则B4的坐标_____，Bn的坐标_____．
【答案】（15，8）， （2n﹣1，2n﹣1）
【解析】
由图和条件可知A1（0，1）A2（1，2）A3（3，4），由此可以求出直线为y=x+1，Bn的横坐标为An+1的横坐标，纵坐标为An的纵坐标，又An的横坐标数列为An=2n-1-1，所以纵坐标为（2n-1），然后就可以求出Bn的坐标为[A（n+1）的横坐标，An的纵坐标，最后根据规律就可以求出B4和Bn的坐标．
解：∵点B1（1，1），B2（3，2），
∴A1（0，1）A2（1，2）A3（3，4），
∴直线y＝kx+b（k＞0）为y＝x+1，
∴Bn的横坐标为An+1的横坐标，纵坐标为An的纵坐标
又An的横坐标数列为An＝2n﹣1﹣1，所以纵坐标为2n﹣1，
∴Bn的坐标为[A（n+1）的横坐标，An的纵坐标]＝（2n﹣1，2n﹣1）．
所以B4的坐标是（24﹣1，23），即（15，8）．
故答案为：（15，8），（2n﹣1，2n﹣1）．
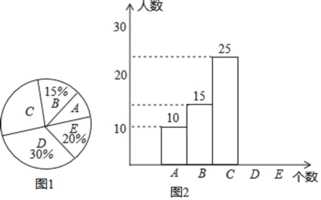
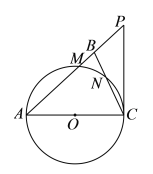
世纪百通主体课堂小学课时同步达标系列答案
【题目】某校举行“汉字听写”比赛，每位学生听写汉字39个．比赛结束后随机抽查部分学生听写结果，图1，图2是根据抽查结果绘制的统计图的一部分．
组别 | 听写正确的个数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息解决下列问题：
（1）本次共随机抽查了多少名学生，求出m，n的值并补全图2的条形统计图；
（2）求出图1中∠α的度数；
（3）该校共有3000名学生，如果听写正确的个数少于24个定为不合格，请你估计这所学校本次比赛听写不合格的学生人数．
