Question

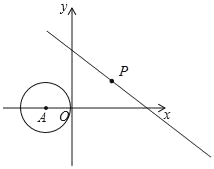
【题目】如图，在平面直角坐标系中，抛物线经过点A（-3，0）、B(2，0)、C(0，4).

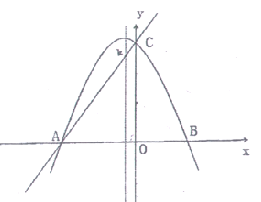
(1)求抛物线的解析式；

(2)在y轴上找一点D，使得△BOD与△AOC相似，请直接写出符合条件的点D的坐标；

(3)若AC与抛物线的对称轴交于点E，以A为圆心，AE长为半径作圆，⊙A与y轴的位置关系如何？请说明理由.

(4)过点E作⊙A的切线EG，交x轴于点G，请求出直线EG的解析式及G点坐标.

Answer 1

【答案】（1）；（2）；（3）⊙A与y轴的位置关系为相交，见解析；（4），G的坐标为.

【解析】

（1）根据抛物线过点A（-3，0）、B(2，0)、C(0，4)，利用待定系数法求解即可.

（2）分△BOD∽△AOC和△BOD∽△COA两种情况，分别利用相似三角形对应边成比例列出比例式，求出OD，即可得到所有符合条件的点D的坐标；

（3）首先求出直线AC的解析式，得到E点坐标，然后可求出AE的长，再与AO作比较即可得出结果；

（4）由直线EG垂直于直线AC可设直线EG的解析式为：，代入E点坐标即可求出解析式，易得G点坐标.

解：（1）设抛物线的解析式为y=ax2+bx+c，

∵抛物线的解析式经过A（-3,0）、B（2,0）、C(0,4).

∴，

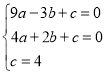解得，

∴抛物线的解析式为；

（2）∵A（-3,0）、B（2,0）、C(0,4)，

∴OA=3，OC=4，OB=2,∠AOC=∠BOC=90°，

①当△BOD∽△AOC时，

则 ，即，

∴OD=，

∴D的坐标为：；

②当△BOD∽△COA时，

则 ，即，

∴OD=

∴D的坐标为：.

综上所述，符合条件的点D的坐标为；

（3）⊙A与y轴的位置关系为相交.

理由如下：

∵直线AC经过A（-3,0）、C(0,4)

∴直线AC的解析式为

∵抛物线的对称轴为直线，AC与抛物线的对称轴交于点E，

∴点E的坐标为，AE=.

∵AO=3，AE=，

∴AO<AE，

∴⊙A与y轴的位置关系为相交

（4）由题意知，直线EG垂直于直线AC，垂足为E，

设直线EG的解析式为：.

∵点在直线上

∴b，即直线EG的解析式为

令中y=0,则

∴点G的坐标为.