��Ŀ����
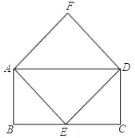
����Ŀ����֪����ABCD��һ����AD��4��������ABCD�۵���ʹ�ö���B���ڱ��ϵ�P�㴦��
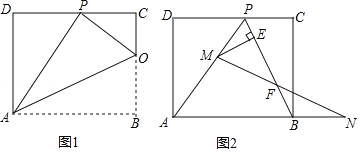
��1����ͼ1����֪�ۺ����BC���ڵ�O������AP��OP��OA����֤����OCP�ס�PDA��
��2������OCP����PDA�������Ϊ1��4�����AB�ij���
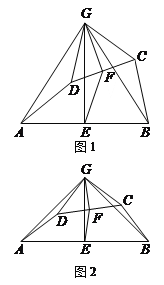
��3����ͼ2���ڣ�1����2���������£���ȥ�ۺ�AO�߶�OP������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN��PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�
���𰸡���1������������2��AB��5����3��EF�ij��Ȳ��䣬EF��![]() ��
��
��������
��1�������۵������ʵõ���APO=��B=90�㣬�������������ε��ж�����֤����OCP�ס�PDA��
��2���������������ε�����ȵ������Ʊȵ�ƽ�����
��3����MQ��AB��PB��Q�����ݵ��������ε����ʺ����������ε����ʵõ�EF=![]() PB�����ݹ��ɶ������PB�����㼴�ɣ�
PB�����ݹ��ɶ������PB�����㼴�ɣ�
��1�����ı���ABCD�Ǿ��Σ�
��AD��BC��DC��AB����DAB����B����C����D��90�㣮
���۵��ɵã�AP��AB��PO��BO����PAO����BAO����APO����B��
���APO��90�㣮
���APD��90�㩁��CPO����POC��
�ߡ�D����C����APD����POC��
���OCP�ס�PDA��
��2���ߡ�OCP�ס�PDA�ҡ�OCP���PDA�������Ϊ1��4
��![]() ,
,
��DA��2CP
��AD��4��
��CP��2
��AB��x����AP��CD��x��DP��x��2��
��Rt��ADP��
�ߡ�D��90�㣬AD��4��DP��x��2��AP��x
��x2����x��2��2+42
��ã�x��5
��AB��5
��3��EF�ij��Ȳ��䣮
��ͼ2����MQ��AB��PB��Q��
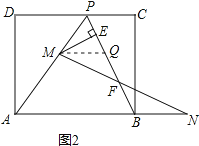
���MQP����ABP��
���۵������ʿ�֪����APB����ABP��
���MQP����APB��
��MP��MQ����BN��PM��
��MQ��BN��
��MQ��AB��
��![]() ��
��
��QF��FB��
��MP��MQ��ME��BP��
��PE��QE��
��EF��![]() PB��
PB��
�ɣ�2���ã�PC��2��BC��4��
��PB��![]() ��
��![]() ��
��
��EF��![]() ��
��