题目内容
【题目】在边长为5的正方形ABCD中,点E,F分别是BC,DC边上的两个动点(不与点B,C,D重合),且AE⊥EF.
(1)如图1,当BE=2时,求FC的长;
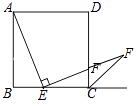
(2)延长EF交正方形ABCD外角平分线CP于点P.
①依题意将图2补全;
②小京通过观察、实验提出猜想:在点E运动的过程中,始终有AE=PE.小京把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的三种想法:
想法1:在AB上截取AG=EC,连接EG,要证AE=PE,需证△AGE≌△ECP.
想法2:作点A关于BC的对称点H,连接BH,CH,EH.要证AE=PE,需证△EHP为等腰三角形.
想法3:将线段BE绕点B顺时针旋转90°,得到线段BM,连接CM,EM,要证AE=PE,需证四边形MCPE为平行四边形.
请你参考上面的想法,帮助小京证明AE=PE.(一种方法即可)
【答案】
(1)
解∵正方形ABCD的边长为5,BE=2,
∴EC=3.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥EF,
∴∠FEC+∠AEB=90°,
∴∠BAE=∠CEF.
∴△ABE∽△ECF,
∴ ![]() ,即
,即 ![]() ,
,
∴FC= ![]()
(2)
解:①依题意补全图形:
②证明:在AB上截取AG=EC,连接EG.
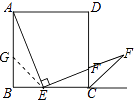
∵AB=BC,
∴GB=EB.
∵∠B=90°,
∴∠BGE=45°,
∴∠AGE=135°.
∵∠DCB=90°,CP是正方形ABCD外角平分线,
∴∠ECP=135°.
∴∠AGE=∠ECP.
在△AGE和△ECP中,
 ,
,
∴△AGE≌△ECP.
∴AE=PE.
【解析】(1)根据正方形的性质求出EC,证明△ABE∽△ECF,根据相似三角形的性质列出比例式,计算即可;(2)①根据题意画图;②在AB上截取AG=EC,连接EG,证明△AGE≌△ECP,根据全等三角形的性质证明.
【考点精析】通过灵活运用全等三角形的性质和相似三角形的性质,掌握全等三角形的对应边相等; 全等三角形的对应角相等;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.