题目内容
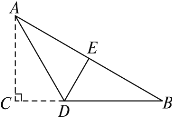
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

【答案】13
【解析】试题分析:根据正方形的性质、直角三角形两个锐角互余以及等量代换可以证得△AFB≌△AED;然后由全等三角形的对应边相等推知AF=DE、BF=AE,所以EF=AF+AE=13.
解:∵ABCD是正方形(已知),
∴AB=AD,∠ABC=∠BAD=90°;
又∵∠FAB+∠FBA=∠FAB+∠EAD=90°,
∴∠FBA=∠EAD(等量代换);
∵BF⊥a于点F,DE⊥a于点E,
∴在Rt△AFB和Rt△AED中,
∵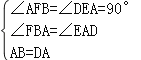 ,
,
∴△AFB≌△AED(AAS),
∴AF=DE=8,BF=AE=5(全等三角形的对应边相等),
∴EF=AF+AE=DE+BF=8+5=13.
故答案为:13.

练习册系列答案
相关题目