Question

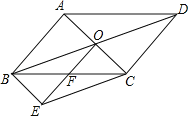
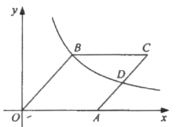
【题目】如图，菱形的顶点在轴上，反比例函数（）的图像经过顶点，和边的中点．若，则的值为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

作BE⊥x轴，DF⊥x轴，根据菱形的性质可得OB∥AC，OB＝AB＝AC＝6，进而可得AD＝AC＝3，由平行可得△BOE∽△DAF，进而可得，设AF＝a，DF＝b，则OE＝2a，BE＝2b，由此可表示出点B、D的坐标，代入函数关系式可得方程，进而可求得k的值．

解：如图，分别过点B、D作BE⊥x轴，DF⊥x轴，垂足分别为E、F，

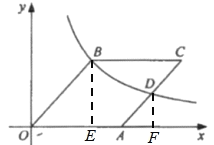
则∠BEO＝∠DFA＝90°，

∵在菱形AOBC中，

∴OB∥AC，OB＝AB＝AC＝6，

∵点D为AC的中点，

∴AD＝AC＝3，

∵OB∥AC，

∴∠BOE＝∠DAF，

∴△BOE∽△DAF，

∴，

∴设AF＝a，DF＝b，

则OE＝2a，BE＝2b，

∴点D（6＋a，b），点B（2a，2b），

∵点B、D均在反比例函数图像上，

∴将点D（6＋a，b），点B（2a，2b）代入得：

b(6＋a)＝2a·2b＝k，

解得a＝2，

∴OE＝2a＝4，

在Rt△BOE中，BE＝，

∴点B（4，），

∴．

故选：D．