题目内容
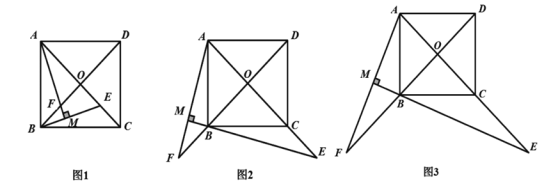
【题目】如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于F.
(1)直接写出线段OE与OF的数量关系;
(2)如图2,若点E在AC的延长线上,过点A作AM⊥BE ,AM交DB的延长线于点F,其他条件不变.问(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,说明理由;
(3)如图3,当BC=CE时,求∠EAF的度数.
【答案】(1) OE=OF; (2) OE=OF仍然成立,理由见解析;(3)67.5°.
【解析】(1)根据正方形的性质利用ASA判定△AOF≌△BOE,根据全等三角形的对应边相等得到OE=OF;
(2)类比(1)的方法证得同理得出结论成立;
(3)由BC=CE, 可证AB=BF,从而∠F=∠FAB=![]() ∠ABD=22.5°,然后根据∠EAF=∠FAB+∠BAO计算即可.
∠ABD=22.5°,然后根据∠EAF=∠FAB+∠BAO计算即可.
(1)OE=OF;
(2)OE=OF仍然成立,理由是:
由正方形ABCD对角线垂直得,∠BOC=90°,
∵AM⊥BE ∴∠BMF=90°,
∴∠BOC=∠BMF.
∵∠MBF=∠OBE,
∴∠F=∠E,
又∵AO=BO,
∴△AOF≌△BOE,
∴OE=OF;
(3)由(2)得OE=OF,且OB=OC,则BF=CE,
∵BC=CE,
∴AB=BF,
∴∠F=∠FAB=![]() ∠ABD=22.5°,
∠ABD=22.5°,
又∵∠BAO=45°,
∴∠EAF=∠FAB+∠BAO=22.5°+45°=67.5°.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目