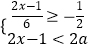题目内容
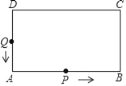
【题目】如图,在长方形ABCD中,AB=14cm,AD=8cm,动点P沿AB边从点A开始,向点B以1cm/s的速度运动;动点Q从点D开始沿DA→AB边,向点B以2cm/s的速度运动.P,Q同时开始运动,当点Q到达B点时,点P和点Q同时停止运动,用t(s)表示运动的时间.
(1)当点Q在DA边上运动时,t为何值,使AQ=AP?
(2)当t为何值时,AQ+AP等于长方形ABCD周长的![]() ?
?
(3)当t为何值时,点Q能追上点P?
【答案】(1)t为![]() 时,AQ=AP.(2)当t为
时,AQ=AP.(2)当t为![]() 或
或![]() 时,AQ+AP等于长方形ABCD周长的
时,AQ+AP等于长方形ABCD周长的![]() .(3)当t为8时,点Q能追上点P.
.(3)当t为8时,点Q能追上点P.
【解析】
(1)找出点Q在DA边上运动且运动时间为ts时,AQ、AP的值,令其相等,即可求出t值;(2)分点Q在DA边上运动时(0≤t≤4)、点Q在AB边上运动时(4≤t≤11)两种情况找出关于t的一元一次方程,解之即可得出结论;(3)点Q追上点P时点Q在AB上运动,令AQ=AP,即可得出关于t的一元一次方程,解之即可得出结论.
(1)当点Q在DA边上运动,运动时间为ts时,AQ=(8﹣2t)cm,AP=tcm,
根据题意得:8﹣2t=t,
解得:t=![]() .
.
答:t为![]() 时,AQ=AP.
时,AQ=AP.
(2)当点Q在DA边上运动时(0≤t≤4),此时AQ=(8﹣2t)cm,AP=t,
根据题意得:8﹣2t+t=2×(14+8)×![]() ,
,
解得:t=![]() ;
;
当点Q在AB边上运动时(4≤t≤11),此时AQ=(2t﹣8)cm,AP=t,
根据题意得:2t﹣8+t=2×(14+8)×![]() ,
,
解得:t=![]() .
.
综上所述:当t为![]() 或
或![]() 时,AQ+AP等于长方形ABCD周长的
时,AQ+AP等于长方形ABCD周长的![]() .
.
(3)根据题意得:2t﹣8=t,
解得:t=8.
答:当t为8时,点Q能追上点P.

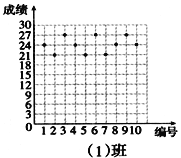
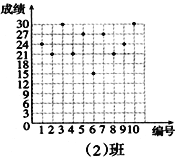
【题目】王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年(1)班和八年(2)班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年(1)班 | 24 | 24 | |
八年(2)班 | 24 |
(2)你认为那个班的学生纠错的得分情况比较整齐一些,通过计算说明理由.