题目内容
【题目】如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm.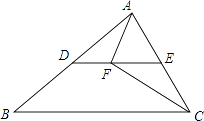
【答案】2
【解析】解:方法一:如图,延长AF交BC于H, 
∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴AF=FH,
∵∠AFC=90°,
∴CF垂直平分AH,
∴CH=AC=6cm,
∵BC=10cm,
∴BH=BC﹣CH=10﹣6=4cm,
在△ABH中,DF是中位线,
∴DF= ![]() BH=
BH= ![]() ×4=2cm;
×4=2cm;
方法二:∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE= ![]() BC=
BC= ![]() ×10=5cm,
×10=5cm,
∵∠AFC=90°,E是AC的中点,
∴EF= ![]() AC=
AC= ![]() ×6=3cm,
×6=3cm,
∴DF=DE﹣EF=5﹣3=2cm.
所以答案是:2.
【考点精析】掌握直角三角形斜边上的中线和三角形中位线定理是解答本题的根本,需要知道直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目