题目内容
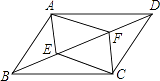
【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
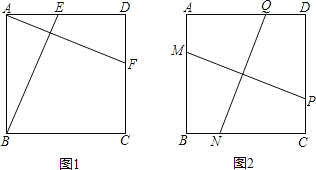
(1)求证:AF=BE;
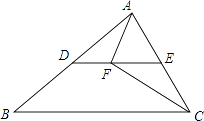
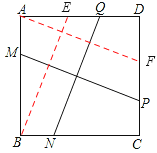
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
【答案】解:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°。
∵AF⊥BE,∴∠ABE+∠BAF=90°。∴∠ABE=∠DAF。
∵在△ABE和△DAF中,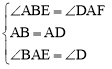 ,
,
∴△ABE≌△DAF(ASA)。
∴AF=BE。
(2)MP与NQ相等。理由如下:
如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则四边形AMPF、BNQE都是是平行四边形,所以,MP=AF,NQ=BE,由(1)AF=BE,即得MP=NQ。
【解析】
试题(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可。
(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则四边形AMPF、BNQE都是是平行四边形,所以,MP=AF,NQ=BE,由(1)AF=BE,即得MP=NQ。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目