题目内容
已知⊙O的半径为2,直线l上有一点P满足OP=2,则直线l与⊙O的位置关系是( )
| A.相切 | B.相离 | C.相切或相离 | D.相切或相交 |
D
试题分析:根据直线与圆的位置关系来判定.判断直线和圆的位置关系:①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r.分OP垂直于直线l,OP不垂直直线l两种情况讨论.解:当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.故直线l与⊙O的位置关系是相切或相交.故答案为:相切或相交
点评:此类试题属于综合性试题,考查直线与圆的位置关系.解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定

练习册系列答案
相关题目

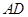 ∶
∶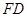 =1∶2,求⊙O的半径的长.
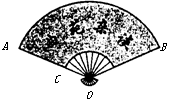
=1∶2,求⊙O的半径的长.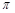 ).
).

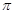 cm2
cm2
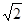 ,∠B=∠DAC,则AC的值为 .
,∠B=∠DAC,则AC的值为 .
