Question

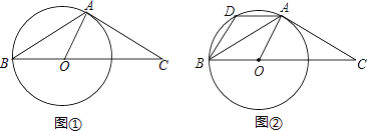
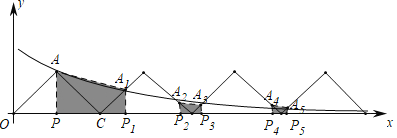
【题目】如图，在△AOC中，∠OAC＝90°，AO＝AC，OC＝2，将△AOC放置于平面直角坐标系中，点O与坐标原点重合，斜边OC在x轴上．反比例函数y＝（x＞0）的图象经过点A．将△AOC沿x轴向右平移2个单位长度，记平移后三角形的边与反比例函数图象的交点为A1，A2．重复平移操作，依次记交点为A3，A4，A5，A6…分别过点A，A1，A2，A3，A4，A5…作x轴的垂线，垂足依次记为P，P1，P2，P3，P4，P5…若四边形APP1A1的面积记为S1，四边形A2P2P3A3的面积记为S2…，则Sn＝_____．（用含n的代数式表示，n为正整数）

Answer 1

【答案】

【解析】

先确定△APC和△A1P1C是等腰直角三角形，四边形APP1A1是直角梯形，设A1P1＝a，则A（1，1），A1（2+a，a），根据点A和A1都在反比例函数的图象上，可列式为1×1＝a（2+a），求出反比例函数解析式和a的值，同理可得结论．

解：∵∠OAC＝90°，AO＝AC，OC＝2，

∴∠AOC＝∠ACO＝45°，

∵AP⊥OC，A1P1⊥x轴，

∴△APC和△A1P1C是等腰直角三角形，四边形APP1A1是直角梯形，

∴AP＝PC＝1，A1P1＝P1C，

设A1P1＝a，则A（1，1），A1（2+a，a），

∴1×1＝a（2+a），a2+2a＝1，（a+1）2＝2，

则反比例函数解析式为：，

，

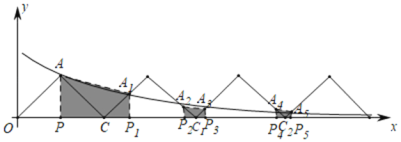
同理得：△A2P2C1和△A3P3C1是等腰直角三角形，四边形A2P2P3A3是直角梯形，

∴A2P2＝P2C1，A3P3＝P3C1，

设A2P2＝b，A3P3＝c，则A2（4﹣b，b），A3（4+c，c），

∴b（4﹣b）＝1，c（4+c）＝1，

∴b＝2+（舍）或2﹣，c＝﹣2﹣（舍）或﹣2+

；

△A4P4C2和△A5P5C2是等腰直角三角形，四边形A4P4P5A5是直角梯形，

∴A4P4＝P4C2，A5P5＝P5C2，

设A4P4＝m，A5P5＝n，则A4（6﹣m，m），A5（6+n，n），

∴m（6﹣m）＝1，n（6+n）＝1，

∴m＝3+（舍）或3﹣，n＝﹣3﹣（舍）或﹣3+，

；

…

∴Sn＝

故答案为：．