题目内容
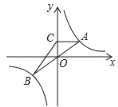
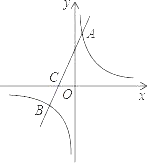
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,与x轴交于点C(﹣2,0),点A的纵坐标为6,AC=3CB.
的图象交于A,B两点,与x轴交于点C(﹣2,0),点A的纵坐标为6,AC=3CB.
(1)求反比例函数的解析式;
(2)请直接写出不等式组![]() <kx+b<4的解集;
<kx+b<4的解集;
(3)点P(x,y)是直线y=k+b上的一个动点,且满足(2)中的不等式组,过点P作PQ⊥y轴交y轴于点Q,若△BPQ的面积记为S,求S的最大值.
【答案】(1)y=![]() ;(2)﹣3<x<0;(3)当m=﹣
;(2)﹣3<x<0;(3)当m=﹣![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
【解析】
(1)作AD⊥x轴、BE⊥x轴,设CE=a,则CD=2+a,证△ACD∽△BCE得![]() ,即
,即![]() ,据此求得a的值即可得出点A的坐标,从而得出反比例函数解析式;
,据此求得a的值即可得出点A的坐标,从而得出反比例函数解析式;
(2)先利用待定系数法求出直线解析式,再结合函数图象可得答案;
(3)设P(m,2m+4)(-3<m<0),知PQ=-m,△BPQ在PQ边上的高为2m+6,根据三角形的面积公式得出S关于m的函数解析式,利用二次函数的性质求解可得.
(1)如图所示,过点A作AD⊥x轴于点D,作BE⊥x轴于点E,
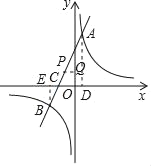
则∠ADC=∠BEC=90°,
设CE=a,则CD=2+a,
∵∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() ,即
,即![]() ,
,
解得:BE=2,a=1,
∴A(1,6),
∴反比例函数解析式为y=![]() ;
;
(2)将A(1,6),C(﹣2,0)代入y=kx+b,
得:![]() ,
,
解得:![]() ,
,
∴直线解析式为y=2x+4,
又B(﹣3,﹣2),
∴不等式组![]() <kx+b<4,即
<kx+b<4,即![]() <2x+4<4的解集为﹣3<x<0;
<2x+4<4的解集为﹣3<x<0;
(3)如图所示,
设P(m,2m+4)(﹣3<m<0),
则PQ=﹣m,△BPQ在PQ边上的高为2m+4﹣(﹣2)=2m+6,
∴S=![]() (﹣m)(2m+6)=﹣m2﹣3m=﹣(m+
(﹣m)(2m+6)=﹣m2﹣3m=﹣(m+![]() )2+
)2+![]() ,
,
∵﹣3<m<0,且抛物线的开口向下,
∴当m=﹣![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.