题目内容
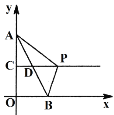
【题目】如图,点A(0,4)、B(2,0),点C、D分别是OA、AB的中点,在射线CD上有一动点P,若△ABP是直角三角形,则点P的坐标为_____.
【答案】(6,2);(1+![]() ,2).
,2).
【解析】
根据勾股定理得到AB=2![]() ,根据三角形中位线的性质得到AC=OC=2,CD=1,AD=BD=
,根据三角形中位线的性质得到AC=OC=2,CD=1,AD=BD=![]() ,①当∠APB=90°时,根据直角三角形的性质得到PD=AD=
,①当∠APB=90°时,根据直角三角形的性质得到PD=AD=![]() ,于是得到P(
,于是得到P(![]() +1,2),②当∠ABP=90°时,如图,过P作PC⊥x轴于C,根据相似三角形的性质得到BP=AB=2
+1,2),②当∠ABP=90°时,如图,过P作PC⊥x轴于C,根据相似三角形的性质得到BP=AB=2![]() ,得到PC=6,求得P(6,2).
,得到PC=6,求得P(6,2).
解:∵点A(0,4),点B(2,0),
∴OA=4,OB=2,
∴AB=2![]() ,
,
∵点C,D分别是OA,AB的中点,
∴AC=OC=2,CD=1,AD=BD=![]() ,
,
①当∠APB=90°时,
∵AD=BD,
∴PD=AD=![]() ,
,
∴PC=CD+PD=![]() +1,
+1,
∴P(![]() +1,2),
+1,2),
②当∠ABP=90°时,如图,

过P作PC⊥x轴于C,
则△ABO∽△BPC,![]()
∴BP=AB=2![]() ,
,
∴PC=OB=2,
∴BC=4,
∴PC=OC=2+4=6,
∴P(6,2),
故答案为:(![]() +1,2)或(6,2).
+1,2)或(6,2).

练习册系列答案
相关题目