题目内容
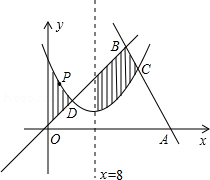
如图,在平面直角坐标系中,直线y=﹣2x+42交x轴于点A,交直线y=x于点B,抛物线y=ax2﹣2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.
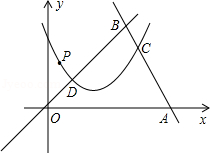
(1)求点C、D的纵坐标.
(2)求a、c的值.
(3)若Q为线段OB上一点,P、Q两点的纵坐标都为5,求线段PQ的长.
(4)若Q为线段OB或线段AB上一点,PQ⊥x轴,设P、Q两点间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围.

(1)求点C、D的纵坐标.
(2)求a、c的值.
(3)若Q为线段OB上一点,P、Q两点的纵坐标都为5,求线段PQ的长.
(4)若Q为线段OB或线段AB上一点,PQ⊥x轴,设P、Q两点间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围.
(1)C的纵坐标为16,D的纵坐标为4,(2)a=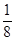 ,c="10" (3)PQ=2
,c="10" (3)PQ=2 ±3(4)0≦m≦4或8≦m≦16.
±3(4)0≦m≦4或8≦m≦16.
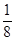 ,c="10" (3)PQ=2
,c="10" (3)PQ=2 ±3(4)0≦m≦4或8≦m≦16.
±3(4)0≦m≦4或8≦m≦16.试题分析:解:(1)∵点C在直线AB:y=﹣2x+42上,且C点的横坐标为16,
∴y=﹣2×16+42=10,即点C的纵坐标为10;
∵D点在直线OB:y=x上,且D点的横坐标为4,
∴点D的纵坐标为4;
(2)由(1)知点C的坐标为(16,10),点D的坐标为(4,4),
∵抛物线y=ax2﹣2x+c经过C、D两点,
∴
 ,
,解得:a=
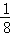 ,c=10,
,c=10,∴抛物线的解析式为y=
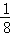 x2﹣2x+10;
x2﹣2x+10;(3)∵Q为线段OB上一点,纵坐标为5,
∴P点的横坐标也为5,
∵点Q在抛物线上,纵坐标为5,
∴
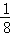 x2﹣2x+10=5,
x2﹣2x+10=5,解得x1=8+2
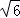 ,x2=8﹣2
,x2=8﹣2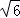 ,
,当点Q的坐标为(8+2
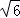 ,5),点P的坐标为(5,5),线段PQ的长为2
,5),点P的坐标为(5,5),线段PQ的长为2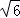 +3,
+3,当点Q的坐标为(8﹣2
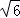 ,5),点P的坐标为(5,5),线段PQ的长为2
,5),点P的坐标为(5,5),线段PQ的长为2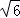 ﹣3.
﹣3.所以线段PQ的长为2
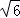 +3或2
+3或2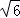 ﹣3.
﹣3.(4)根据题干条件:PQ⊥x轴,可知P、Q两点的横坐标相同,
抛物线y=
 x2﹣2x+10=
x2﹣2x+10= (x﹣8)2+2的顶点坐标为(8,2),
(x﹣8)2+2的顶点坐标为(8,2),联立
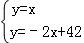 解得点B的坐标为(14,14),
解得点B的坐标为(14,14),①当点Q为线段OB上时,如图所示,当0≤m≤4或8≤m≤14时,d随m的增大而减小,
②当点Q为线段AB上时,如图所示,当14≤m≤16时,d随m的增大而减小,
综上所述,当0≤m≤4或8≤m≤16时,d随m的增大而减小.
点评:熟知以上性质,本题有四问较多,计算量也很大,需要细心审题解答,综合性较强,易出错,本题难度偏大,复杂,属于难题。

练习册系列答案
相关题目
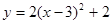 的图象下列叙述正确的是( )
的图象下列叙述正确的是( ) =3
=3 有最大值2
有最大值2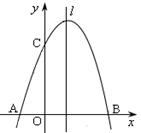
 时,求直线AN的解析式.
时,求直线AN的解析式. 与直线
与直线 相交于O(0,0)和A(3,2)两点,则不等式
相交于O(0,0)和A(3,2)两点,则不等式 的解集为 .
的解集为 .
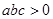 ;②
;②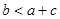 ; ③
; ③ ;④
;④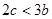 ;⑤
;⑤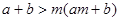
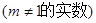 其中正确的是( )
其中正确的是( )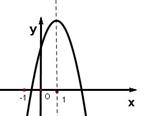
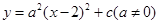 ,当自变量x分别取0,
,当自变量x分别取0,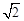 ,3时,对应的值分别为
,3时,对应的值分别为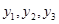 ,则
,则 的对称轴是直线
的对称轴是直线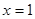 ,且经过点
,且经过点 (3,0),则
(3,0),则 的值为( )
的值为( )