题目内容
【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
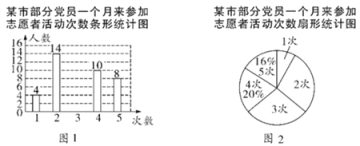
(1) “![]() 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;
(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于![]() 次的概率;
次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为![]() ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为![]() ,当
,当![]() 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数.
【答案】(1)![]() ,补全条形统计图如解图所示见解析;(2)
,补全条形统计图如解图所示见解析;(2)![]() (该党员一个月来参加志愿者活动次数不少于
(该党员一个月来参加志愿者活动次数不少于![]() 次)
次)![]() ;(3)去掉
;(3)去掉![]() 个参加志愿者活动次数为
个参加志愿者活动次数为![]() 次的和
次的和![]() 个参加志愿者活动次数为
个参加志愿者活动次数为![]() 次的.
次的.
【解析】
(1)根据扇形统计图可知“4次”的人数占比为20%,即可出圆心角度数;根据“4次”人数占比,求出总人数,进而可以求得“3”次的人数;
(2)![]() (该党员一个月来参加志愿者活动次数不少于
(该党员一个月来参加志愿者活动次数不少于![]() 次)=少于3次的人数
次)=少于3次的人数![]() 总人数;
总人数;
(3)首先求出中位数![]() ,根据题意,使得新数据的众数
,根据题意,使得新数据的众数![]()
![]() ,得到b=4或者5,再比较需要去掉的人数,取最少去掉的人数即可.
,得到b=4或者5,再比较需要去掉的人数,取最少去掉的人数即可.
(1)由扇形统计图知“4次”的人数占比为20%,
∴“4次”所在圆心角的度数为360![]() 20%=72
20%=72![]() .
.
随机抽查的党员人数为 ![]() (人),
(人),
∴“3次”的人数为50-4-14-10-8=14(人)
补全条形统计图如图所示:
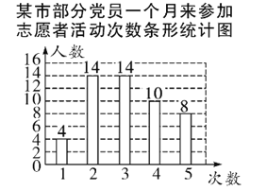
(2)∵随机抽查的党员人数为 ![]() (人),其中参加志愿者活动次数不少于
(人),其中参加志愿者活动次数不少于![]() 次的有14+10+8=32(人),
次的有14+10+8=32(人),
∴P(该党员一个月来参加志愿者活动次数不少于3次)![]() .
.
(3)将参加次数按由小到大进行排列,可得中位数为第25、26个数的平均数,由题意得![]() ,
,
∵去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为![]() ,且
,且![]() ,
,
∴![]() 或5,当
或5,当![]() 时,最少需去掉10名党员参加志愿者活动的次数,
时,最少需去掉10名党员参加志愿者活动的次数,
即去掉![]() 个参加志愿者活动次数为
个参加志愿者活动次数为![]() 次的和
次的和![]() 个参加志愿者活动次数为
个参加志愿者活动次数为![]() 次的,
次的,
当![]() 时,最少需去掉17名党员参加志愿者活动的次数,
时,最少需去掉17名党员参加志愿者活动的次数,
即去掉7个参加活动为2次的,7个参加活动为3次的,3个参加活动为4次的,
∵10![]() 17
17
∴b=4.
这时最少去掉了10名党员这一个月来参加志愿者活动的次数.
即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案




