Question

【题目】已知，在中，，点为边上一动点，且，连接，其中．

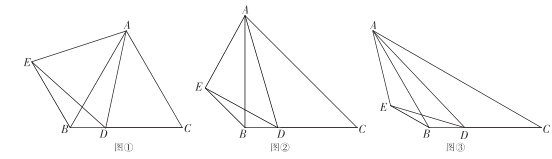
问题发现：（1）如图1，若，与有怎样的数量关系？的值为多少？直接写出答案；

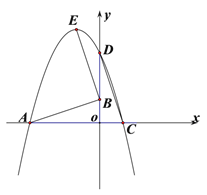
类比探究，（2）如图2，若，点在的延长线上，与有怎样的数量关系？的值为多少？请说明理由．

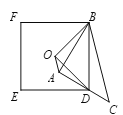
拓展应用：（3）如图3，在中，，，为上一点，以为边，在如图所示位置作正方形，点为正方形的对称中心，且，请直接写出的长．

Answer 1

【答案】（1）∠BCE＝∠A＝60°；k＝1；（2）∠BCE＝∠A，k＝，理由见解析；（3）

【解析】

（1）证明，得，即可得解；

（2）先证明△ABC∽△DBE，，结合∠ABD＝∠CBE，根据对应边成比例且夹角相等可证明△ABD∽△CBE，即可得出结论；

（3）连接BO、OD，通过证明∽，再根据相似三角形对应边成比例，求出DC，进而求出AD，再利用勾股定理求DB，则DE=DB．

解：（1）∵， ，

∴为等边三角形，

∴，，

又∵且，

∴为等边三角形，

∴，，

∴，

在和中，

∴，

∴，，

∴

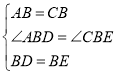
故答案为：，．

（2）∠BCE＝∠A，k＝．

理由如下：∵∠BAC＝∠BDE，AB＝AC，BD＝DE，

∴∠ABC＝∠DBE，

∴△ABC∽△DBE，

∴，

又∵∠ABC＋∠CBD＝∠DBE＋∠CBD，即∠ABD＝∠CBE

∴△ABD∽△CBE（对应边成比例，夹角相等），

∴，；

（3）如图，连接BO、OD，

∵四边形为正方形，点为正方形的对称中心，

∴，，

∵为等腰直角三角形，

∴，，

∴，

∴∽，

∴，即，

∴，

∴，

∴，

故的长为：．