ΧβΡΩΡΎ»ί
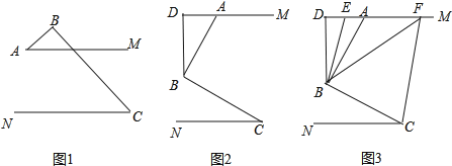
ΓΨΧβΡΩΓΩ“ΜΗωœδΉ”ΡΎ”–4Ω≈œύΆ§ΒΡ«ρΘ§ΫΪ4Ω≈«ρΖ÷±π±ξ ΨΚ≈¬κ1ΓΔ2ΓΔ3ΓΔ4Θ§Ϋώœηœη“‘ΟΩ¥Έ¥”œδΉ”ΡΎ»Γ“ΜΩ≈«ρ«“»ΓΚσΖ≈ΜΊΒΡΖΫ Ϋ≥ι»ΓΘ§≤Δ‘ΛΦΤ»Γ«ρ10¥ΈΘ§œ÷“―»ΓΝΥ8¥ΈΘ§»Γ≥ωΒΡΫαΙϊ»γ±μΥυΝ–ΘΚ
¥Έ ΐ | ΒΎ1¥Έ | ΒΎ2¥Έ | ΒΎ3¥Έ | ΒΎ4¥Έ | ΒΎ5¥Έ | ΒΎ6¥Έ | ΒΎ7¥Έ | ΒΎ8¥Έ | ΒΎ9¥Έ | ΒΎ10¥Έ |
Κ≈¬κ | 1 | 3 | 4 | 4 | 2 | 1 | 4 | 1 |
»τΟΩ¥Έ»Γ«ρ ±Θ§»Έ“ΜΩ≈«ρ±Μ»ΓΒΫΒΡΜζΜαΫ‘œύΒ»Θ§«“»Γ≥ωΒΡΚ≈¬κΦ¥ΈΣΒΟΖ÷Θ§«κΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«κ«σ≥ωΒΎ1¥Έ÷ΝΒΎ8¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐΘ°
Θ®2Θ©≥–Θ®1Θ©Θ§œηœη¥ρΥψ“άΦΤΜ°ΦΧ–χ¥”œδΉ”»Γ«ρ2¥ΈΘ§«κ≈–Εœ «ΖώΩ…ΡήΖΔ…ζΓΗ’β10¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ≤Μ–Γ”Ύ2.2Θ§«“≤Μ¥σ”Ύ2.4ΓΙΒΡ«ι–ΈΘΩ»τ”–Ω…ΡήΘ§«κΦΤΥψ≥ωΖΔ…ζ¥Υ«ι–ΈΒΡΜζ¬ Θ§≤ΔΆξ’ϊ–¥≥ωΡψΒΡΫβΧβΙΐ≥ΧΘΜ»τ≤ΜΩ…ΡήΘ§«κΆξ’ϊΥΒΟςΡψΒΡάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΒΎ1¥Έ÷ΝΒΎ8¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ «2.5ΘΜΘ®2Θ©ΚσΝΫ¥ΈΒΡΒΟΖ÷≤Μ–Γ”Ύ2ΓΔ≤Μ¥σ”Ύ4ΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΗυΨίΥψ θΤΫΨυ ΐΒΡΕ®“εΝ– ΫΦΤΥψΩ…ΒΟΘΜ
Θ®2Θ©œ»ΗυΨί’β10¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ≤Μ–Γ”Ύ2.2Θ§«“≤Μ¥σ”Ύ2.4ΒΟ≥ωΚσΝΫ¥ΈΒΟΖ÷ΒΡΖΕΈßΘ§‘ΌΝ–±μΒΟ≥ωΥυ”–Β»Ω…ΡήΫαΙϊΘ§¥”÷–’“¥ρΖϊΚœΧθΦΰΒΡΫαΙϊ ΐΘ§άϊ”ΟΗ≈¬ ΙΪ ΫΦΤΥψΩ…ΒΟΘ°
Θ®1Θ©ΒΎ1¥Έ÷ΝΒΎ8¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ![]() =2.5ΘΜ
=2.5ΘΜ
Θ®2Θ©ΓΏ’β10¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ≤Μ–Γ”Ύ2.2Θ§«“≤Μ¥σ”Ύ2.4Θ§
Γύ’β10¥ΈΒΟΖ÷÷°ΚΆ≤Μ–Γ”Ύ22ΓΔ≤Μ¥σ”Ύ24Θ§
Εχ«Α8¥ΈΒΡΒΟΖ÷÷°ΚΆΈΣ20Θ§
ΓύΚσΝΫ¥ΈΒΡΒΟΖ÷÷°ΚΆ≤Μ–Γ”Ύ2ΓΔ≤Μ¥σ”Ύ4Θ§
Ν–±μΒΟΘΚ
Θ®1Θ§4Θ© | Θ®2Θ§4Θ© | Θ®3Θ§4Θ© | Θ®4Θ§4Θ© |
Θ®1Θ§3Θ© | Θ®2Θ§3Θ© | Θ®3Θ§3Θ© | Θ®4Θ§3Θ© |
Θ®1Θ§2Θ© | Θ®2Θ§2Θ© | Θ®3Θ§2Θ© | Θ®4Θ§2Θ© |
Θ®1Θ§1Θ© | Θ®2Θ§1Θ© | Θ®3Θ§1Θ© | Θ®4Θ§1Θ© |
Γύ“ΜΙ≤”–16÷÷«ιΩωΘ§Τδ÷–ΒΟΖ÷÷°ΚΆ≤Μ–Γ”Ύ2ΓΔ≤Μ¥σ”Ύ4ΒΡ”–6÷÷ΫαΙϊΘ§
’β10¥ΈΒΟΖ÷ΒΡΤΫΨυ ΐ≤Μ–Γ”Ύ2.2Θ§«“≤Μ¥σ”Ύ2.4ΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ»γΆΦ «”Ο≥ΛΕ»œύΒ»ΒΡ–ΓΑτΑ¥“ΜΕ®Ιφ¬…ΑΎ≥…ΒΡ“ΜΉιΆΦΑΗ

Θ®1Θ©Χν–¥œ¬±μΘΚ
ΆΦ–Έ–ρΚ≈ | ΔΌ | ΔΎ | Δέ | Γ≠Γ≠ | Δύ |
ΟΩΗωΆΦΑΗ÷––ΓΑτΒΡ ΐΝΩ | 6 | 11 | Γ≠Γ≠ |
Θ®2Θ©«κΧν–¥≥ωΒΎ![]() ΗωΆΦΑΗ÷––ΓΑτΒΡ ΐΝΩΘ®”ΟΚ§
ΗωΆΦΑΗ÷––ΓΑτΒΡ ΐΝΩΘ®”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®3Θ©ΒΎ30ΗωΆΦΑΗ÷––ΓΑτ”–Εύ…ΌΗυΘΩ
ΓΨΧβΡΩΓΩΡ≥ΩΨ―ΦΒξ‘Ύ»ΖΕ®ΩΨ―ΦΒΡΩΨ÷Τ ±Φδ ±Θ§÷ς“Σ“άΨίΒΡ «œ¬±μΒΡ ΐΨίΘΚ
―ΦΒΡ÷ ΝΩ/«ßΩΥ | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
ΩΨ÷Τ ±Φδ/Ζ÷ | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
…η―ΦΒΡ÷ ΝΩΈΣx«ßΩΥΘ§ΩΨ÷Τ ±ΦδΈΣtΘ§ΙάΦΤΒ±x=2.8«ßΩΥ ±Θ§tΒΡ÷ΒΈΣΘ® Θ©
A. 128B. 132C. 136D. 140