Question

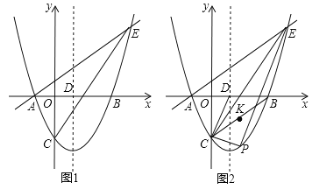
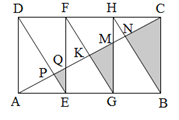
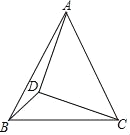
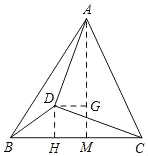
【题目】如图，在△ABC中，AB=AC，tan∠ACB=2，D在△ABC内部，且AD=CD，∠ADC=90°，连接BD，若△BCD的面积为10，则AD的长为多少？

Answer 1

【答案】5

【解析】

作辅助线构建全等三角形和高线DH，设CM=a，根据等腰直角三角形的性质和三角函数表示AC和AM的长，根据三角形面积表示DH的长，证明△ADG≌△CDH，得出DG和AG的长度，即可得出答案.

解：过D作DH⊥BC于H，过A作AM⊥BC于M，过D作DG⊥AM于G，

设CM=a，

∵AB=AC，

∴BC=2CM=2a，

∵tan∠ACB=2，

∴=2，

∴AM=2a，

由勾股定理得：AC=a，

S△BDC=BCDH=10，

=10，

DH=，

∵∠DHM=∠HMG=∠MGD=90°，

∴四边形DHMG为矩形，

∴∠HDG=90°=∠HDC+∠CDG，DG=HM，DH=MG，

∵∠ADC=90°=∠ADG+∠CDG，

∴∠ADG=∠CDH，

在△ADG和△CDH中，

∵，

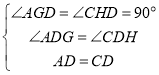∴△ADG≌△CDH（AAS），

∴DG=DH=MG=，AG=CH=a+，

∴AM=AG+MG，

即2a=a++，

a2=20，

在Rt△ADC中，AD2+CD2=AC2，

∵AD=CD，

∴2AD2=5a2=100，

∴AD=或（舍），

故答案为：