题目内容
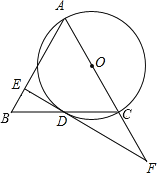
【题目】如图示,![]() 是
是![]() 的直径,点
的直径,点![]() 是半圆上的一动点(
是半圆上的一动点(![]() 不与
不与![]() ,
,![]() 重合),弦
重合),弦![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
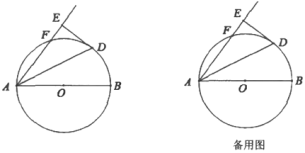
(1)求证:![]() 与
与![]() 相切:
相切:
(2)若![]() ,
,![]() ,求
,求![]() 长;
长;
(3)若![]() ,
,![]() 长记为
长记为![]() ,
,![]() 长记为
长记为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值.
的最大值.
【答案】(1)详见解析;(2)4;(3)![]()
【解析】
(1)首先连接![]() ,通过半径和角平分线的性质进行等角转换,得出
,通过半径和角平分线的性质进行等角转换,得出![]() ,进而得出
,进而得出![]() ,即可得证;
,即可得证;
(2)首先连接![]() ,得出
,得出![]() ,进而得出
,进而得出![]() ,再根据勾股定理得出DE;
,再根据勾股定理得出DE;
(3)首先连接![]() ,过点
,过点![]() 作
作![]() ,得出
,得出![]() ,再得
,再得![]() ,进而得出
,进而得出![]() ,然后构建二次函数,即可得出其最大值.
,然后构建二次函数,即可得出其最大值.
(1)证明:连接![]()
∵![]()
∴![]()
∵![]() 平分
平分![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
又∵![]() 是
是![]() 的半径
的半径
∴![]() 与
与![]() 相切
相切
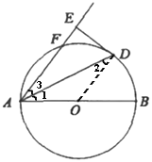
(2)解:连接![]()
∵AB为直径
∴∠ADB=90°
∵![]()
∴![]()
∴![]()
∴![]()
∴![]() 中
中![]()
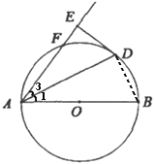
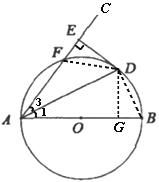
(3)连接![]() ,过点
,过点![]() 作
作![]() 于
于![]()
∵![]() ,DE⊥AE,AD=AD
,DE⊥AE,AD=AD
∴![]()
∴![]() ,DE=DG
,DE=DG
∴![]()
∴![]()
∴![]()
即:![]()
∴![]()
∴![]()
根据二次函数知识可知:当![]() 时,
时,![]()

练习册系列答案
相关题目