题目内容
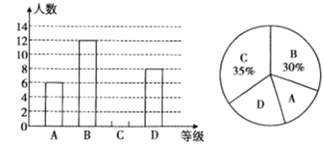
【题目】如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( ).
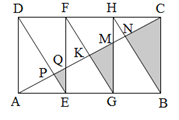
A.6B.8
C.10D.12
【答案】D
【解析】
根据矩形的性质和平行四边形的性质判断出△AQE∽△AMG∽△ACB,得到![]() ,
,![]() ,再通过证明得到△PQE∽△KMG∽△NCB,利用面积比等于相似比的平方,得到S1、S2、S3的关系,进而可得到答案.
,再通过证明得到△PQE∽△KMG∽△NCB,利用面积比等于相似比的平方,得到S1、S2、S3的关系,进而可得到答案.
解:∵矩形ABCD是由三个全等矩形拼成的,
∴AE=EG=GB=DF=FH=HC,∠AEQ=∠AGM=∠ABC=90°,AB∥CD,AD∥EF∥GH∥BC
∴∠AQE=∠AMG=∠ACB,
∴△AQE∽△AMG∽△ACB,![]()
∴![]() ,
,![]()
∵EG= DF=GB=FH AB∥CD,(已证)
∴四边形DEGF,四边形FGBH是平行四边形,
∴DE∥FG∥HB
∴∠QPE=∠MKG=∠CNB,
∴△PQE∽△KMG∽△NCB
∴![]()
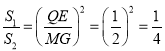
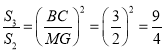 ,
,
∴![]() ,
,![]()
∵S1+S3=30,
∴S2=12.
故选:D.

练习册系列答案
相关题目
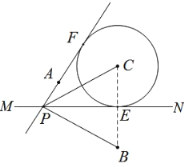
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
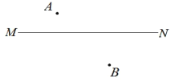
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.