题目内容
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上.
上.
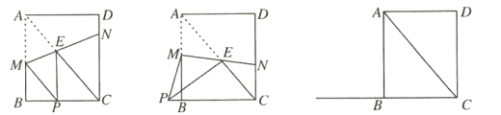
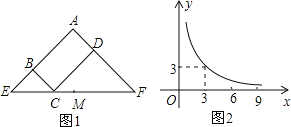
(1)如图1所示,当![]() 时,求
时,求![]() 的长;
的长;
(2)如图2所示,当![]() 时,求
时,求![]() 的长;
的长;
(3)请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据翻折性质可得![]() ,得
,得![]() ,
,![]() .结合矩形性质得证
.结合矩形性质得证![]() ,根据平行线性质得
,根据平行线性质得![]() .
.![]() .设
.设![]() .得
.得![]() ,由
,由![]()
![]() 可求出x;
可求出x;
(2)结合(1)方法可得![]() ,
,![]() ,再根据勾股定理求PC,再求
,再根据勾股定理求PC,再求![]() ,
,![]() 中,
中,![]() ;
;
(3)作图当P与C重合时,PC最小,是0;当N与C重合时,PC最大=![]() .
.
解:(1)![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,
处,
![]() .
.
![]() ,
,![]() .
.
∵四边形![]() 是矩形,
是矩形,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
∵四边形![]() 是矩形,
是矩形,![]() .
.
![]() .
.
![]() .设
.设![]() .
.
∵四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]()
![]() .
.
解得![]() ,
,
即![]() .
.
(2)![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,
处,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,
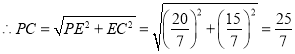 .
.
![]()
![]() .
.
在![]() 中,
中,
![]() ,
,![]() .
.
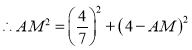 .
.
![]() .
.
(3)如图当P与C重合时,PC最小,是0;
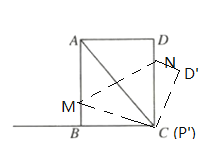
如图当N与C重合时,PC最大=![]() =
=![]() =5;
=5;
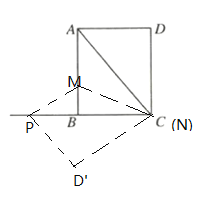
所以![]() ,此时PB=2,设PM=x,则BM=4-x
,此时PB=2,设PM=x,则BM=4-x
由PB2+BM2=PM2可得22+(4-x)2=x2
解得x=![]() , BM=4-x=
, BM=4-x=![]()
所以MN=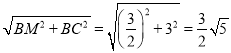
综合上述:![]() ,当
,当![]() 最大时
最大时![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目