题目内容
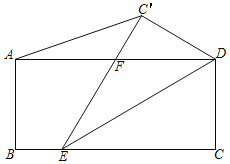
【题目】在矩形ABCD中,AB=3,BC=2![]() ,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
A.![]() B.2
B.2![]() C.2
C.2![]() D.
D.![]() +1
+1
【答案】A
【解析】
过点C'作C'H⊥AD于点H,由折叠的性质可得CD=C'D=3,∠C=∠EC'D=90°,由勾股定理可求C'F=1,由三角形面积公式可求C'H的长,再由勾股定理可求AC'的长.
解:如图,过点C'作C'H⊥AD于点H,
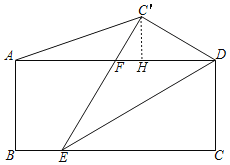
∵点F为AD的中点,AD=BC=2![]()
∴AF=DF=![]()
∵将△DEC沿DE翻折
∴CD=C'D=3,∠C=∠EC'D=90°
在Rt△DC'F中,C'F=![]()
∵S△C'DF=![]()
∴![]() ×C'H=1×3
×C'H=1×3
∴C'H=![]()
∴FH=![]()
∴AH=AF+FH=![]()
在Rt△AC'H中,AC'=![]()
故选:A.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目